A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral. The circle which consists of all the vertices of any polygon on its circumference is known as the circumcircle or circumscribed circle.
| Table of contents: |
A quadrilateral is a 4 sided polygon bounded by 4 finite line segments. The word ‘quadrilateral’ is composed of two Latin words, Quadri meaning ‘four ‘and latus meaning ‘side’. It is a two-dimensional figure having four sides (or edges) and four vertices. A circle is the locus of all points in a plane which are equidistant from a fixed point.
If all the four vertices of a quadrilateral ABCD lie on the circumference of the circle, then ABCD is a cyclic quadrilateral. In other words, if any four points on the circumference of a circle are joined, they form the vertices of a cyclic quadrilateral. It can be visualized as a quadrilateral which is inscribed in a circle, i.e. all four vertices of the quadrilateral lie on the circumference of the circle.
Cyclic Quadrilateral Definition
The definition states that a quadrilateral which is circumscribed in a circle is called a cyclic quadrilateral. It means that all the four vertices of quadrilateral lie in the circumference of the circle. Let us understand with a diagram.
In the figure given below, the quadrilateral ABCD is cyclic.

Let us do an activity. Take a circle and choose any 4 points on the circumference of the circle. Join these points to form a quadrilateral. Now measure the angles formed at the vertices of the cyclic quadrilateral. It is noted that the sum of the angles formed at the vertices is always 360o and the sum of angles formed at the opposite vertices is always supplementary.
Read more:
Cyclic Quadrilateral Angles
The sum of the opposite angles of a cyclic quadrilateral is supplementary.
Let ∠A, ∠B, ∠C and ∠D are the four angles of an inscribed quadrilateral. Then,
∠A + ∠C = 180°
∠B + ∠D = 180°
Therefore, an inscribed quadrilateral also meets the angle sum property of a quadrilateral, according to which, the sum of all the angles equals 360 degrees. Hence,
Radius of Cyclic Quadrilateral
If a, b, c and d are the successive sides of a cyclic quadrilateral, and s is the semi perimeter, then the radius is given by,
Diagonals of Cyclic Quadrilaterals
Suppose a,b,c and d are the sides of a cyclic quadrilateral and p & q are the diagonals, then we can find the diagonals of it using the below given formulas:
Area of Cyclic Quadrilateral
If a,b,c and d are the sides of a inscribed quadrialteral, then its area is given by:
Where s is the semiperimeter.
Cyclic Quadrilateral Theorems
There are two important theorems which prove the cyclic quadrilateral.
Theorem 1
In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.
Proof: Let us now try to prove this theorem.
Given: A cyclic quadrilateral ABCD inscribed in a circle with center O.
Construction: Join the vertices A and C with center O.
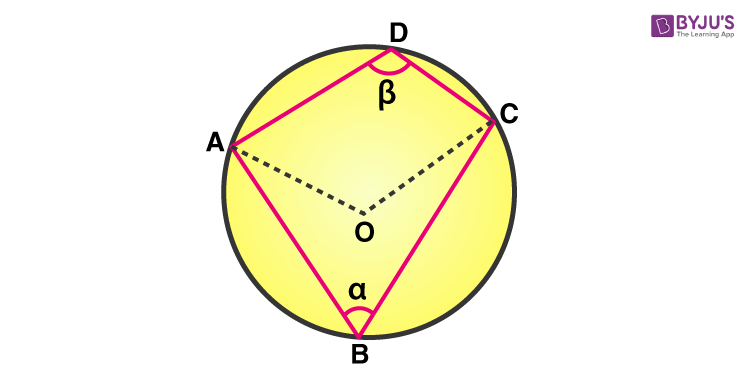
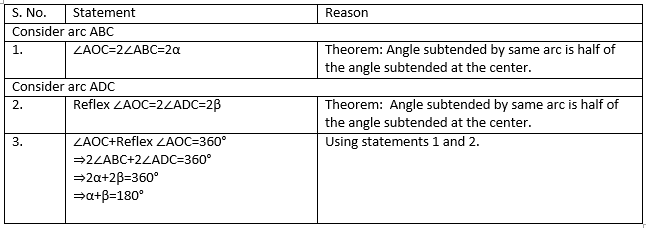
The converse of this theorem is also true, which states that if opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
Theorem 2
The ratio between the diagonals and the sides can be defined and is known as Cyclic quadrilateral theorem. If there’s a quadrilateral which is inscribed in a circle, then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.
If PQRS is a cyclic quadrilateral, PQ and RS, and QR and PS are opposite sides. PR and QS are the diagonals.
(PQ x RS) + ( QR x PS) = PR x QS

Properties of Cyclic Quadrilateral
|
|
|
|
|
|
|
|
|
|
|
Problems and Solutions
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 60o.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
60° + ∠D = 180°
∠D = 180° – 60°
∠D = 120°
The value of angle D is 120°.
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 80°.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
80° + ∠D = 180°
∠D = 180° – 80°
∠D = 100°
The value of angle D is 100°.
You should practise more examples using cyclic quadrilateral formulas to understand the concept better.
Register at BYJU’S to practise, solve and understand other mathematical concepts in a fun and engaging way.
Video Lesson


Comments