Integration by Partial Fractions

Integration by partial fractions is one of the methods of integrating complex functions. Before learning about the integration process by partial fractions, first, understand the meaning of partial fractions and how to write the partial fractions. Partial fractions are the sum of proper rational functions obtained when we decompose an improper rational function. Here, the improper rational function means the rational function with the degree of its numerator is not less than the degree of the denominator. Different formulas are available to decompose improper rational functions and get partial fractions.

Click here to understand more about rational functions and partial fractions.

Integration by the Partial Fractions Method

We can observe rational functions as integrands in the process of integration. In this case, we must reduce the integration of any rational function to the integration of a proper rational function. The rational functions we shall consider here for integration purposes will be those whose denominators can be factored into linear and quadratic factors. The method of writing the integrand, an improper rational function as a sum of simpler rational functions, is called partial fraction decomposition. Finding the integral in such cases is called integration by partial fraction method. This method of integration is simple and can be done using easy steps and formulas.

Integration by Partial Fractions Formula

The list of formulas used to decompose the given improper rational functions is given below. Using these expressions, we can quickly write the integrand as a sum of proper rational functions.

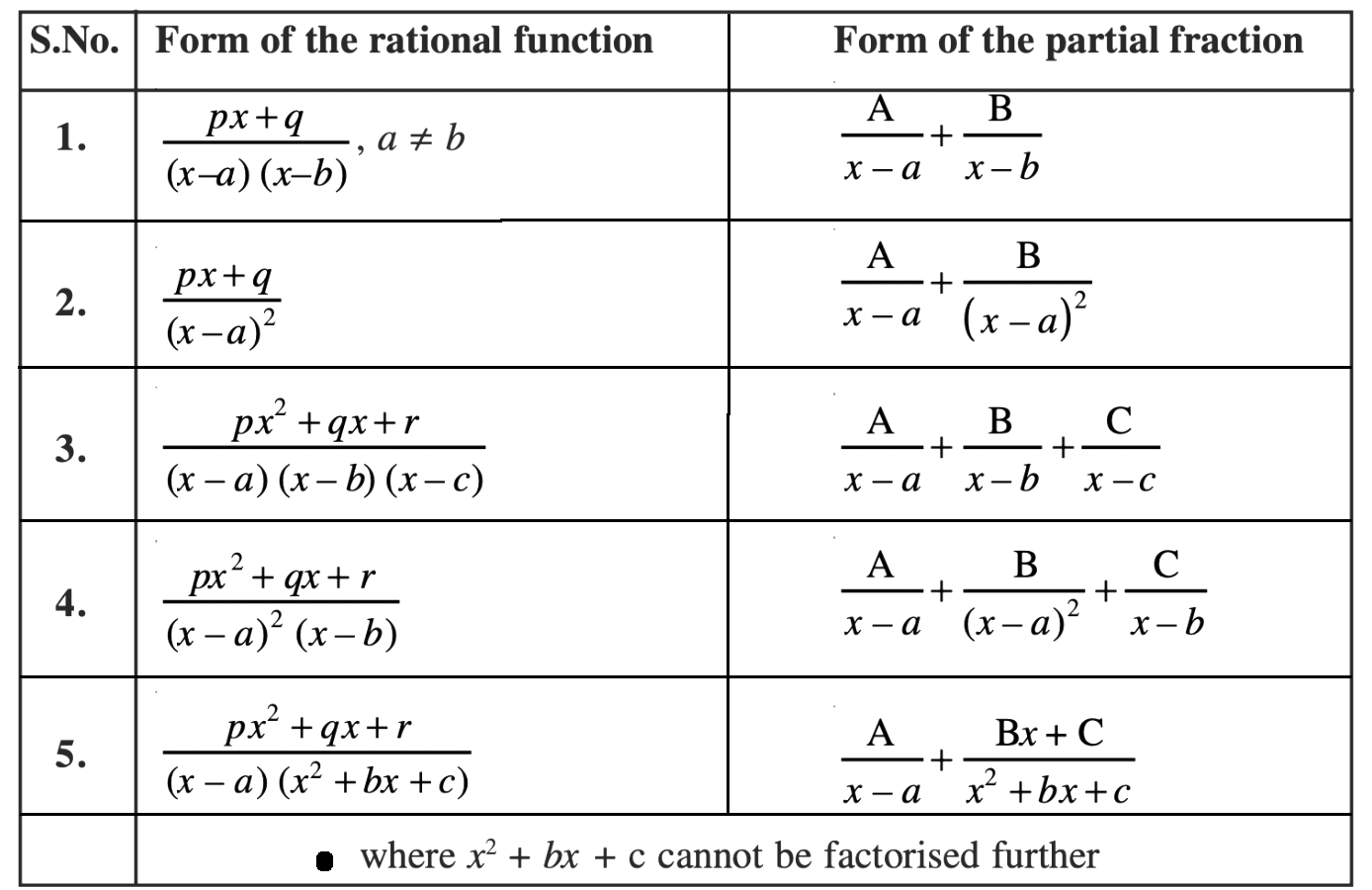
Also, get: Partial Fractions Decomposition Calculator

How to do Integration by Partial Fractions?

Go through the steps given below to understand the integration process by partial fractions.

Step 1: Check whether the given integrand is a proper or improper rational function.

Step 2: If the given function is an improper rational function, identify the type of denominator.

Step 3: Decompose the integrand using a suitable expression by comparing it with the five different forms given above.

Step 4: Now, divide the integration into parts and integrate the individual functions.

This can be understood in a better way with the help of solved examples given below:

Integration by Partial Fractions Examples and Solutions

Example 1:

Evaluate:

Solution:

Given,

Step 1: Integrand =

Step 2: This type of integrand is not specified in the table above, so divide the numerator by denominator.

Thus,

Now, factorising the denominator, we get; x² – 5x + 6 = (x – 2)(x – 3)

So,

Step 3: Let us decompose the obtained proper rational fraction.

We know that, (px+q)/(x – a)(x – b) = A/(x – a) + B/(x – b); a ≠ b

From this, we can write (5x – 5)/(x – 2)(x – 3) as:

By equating the numerators, we get;

5x – 5 = A(x – 3) + B(x – 2)

5x – 5 = Ax – 3A + Bx – 2B

5x – 5 = (A + B)x – (3A + 2B)

Thus, A + B = 5….(i)

3A + 2B = 5….(ii)

From 3×(i) – (ii),

3A + 3B – 3A – 2B = 15 – 5

B = 10

Substituting B = 10 in (i),

A = 5 – 10 = -5

Now, we can write the integrand as:

Step 4:

= x – 5 log|x – 2| + 10 log|x – 3| + C

Example 2:

Find

Solution:

Given,

The given integrand is an improper rational function.

Let us decompose this into the sum of proper rational functions.

Now, equate the numerators.

x = A(x – 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x – 2)

x = A(x² – 5x + 6) + B(x² – 4x + 3) + C(x² – 3x + 2)

x = (A + B + C)x² – (5A + 4B + 3C)x + (6A + 3B + 2C)

By equating the coefficients of the terms, we get;

A + B + C = 0….(i)

5A + 4B + 3C = -1….(ii)

6A + 3B + 2C = 0….(iii)

From (ii),

2A + B + 3(A + B + C) = -1

2A + B + 0 = -1

2A + B = -1….(iv)

From (iii),

4A + B + 2(A + B + C) = 0

4A + B + 0 = 0

B = -4A….(v)

From (iv) and (v),

2A – 4A = -1

-2A = -1

A = ½

B = -4(½) = -2

C = -(½) + 2 = 3/2

Substituting these values in the decomposed form of the integrand, we get;

Thus,

= (½) log|x – 1| – 2 log|x – 2| + (3/2) log|x – 3| + C

Practice Questions

Integrate the following functions by the method of partial fractions.

1. 1/(x⁴ – 1)
2. x/(x – 1)²(x + 2)
3. (x³ + x + 1)/(x² – 1)
4. (3x – 1)/ (x – 1)(x – 2)(x – 3)

To learn more integration methods, visit byjus.com, and get more practice questions and solved examples.