In Mathematics, a linear function is defined as a function that has either one or two variables without exponents. It is a function that graphs to the straight line. In case, if the function contains more variables, then the variables should be constant, or it might be the known variables for the function to remain it in the same linear function condition. In this article, we are going to discuss what is a linear function, its table, graph, formulas, characteristics, and examples in detail.
Table of Contents:
What is a Linear Function?
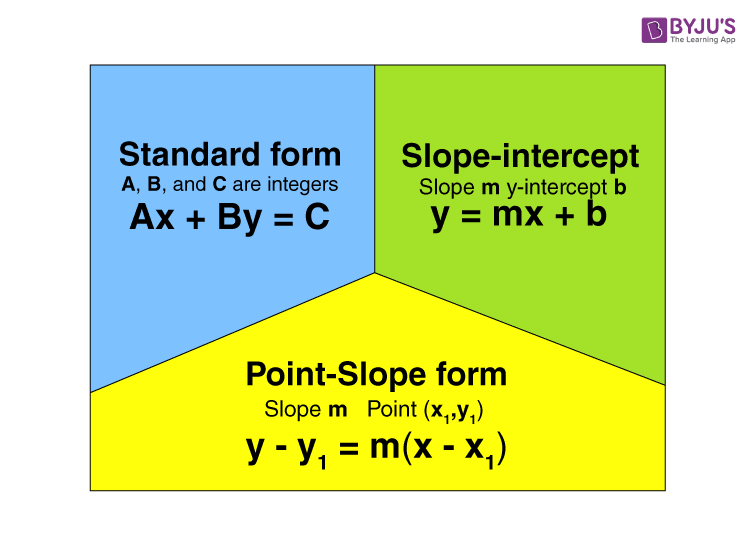
A linear function is a function which forms a straight line in a graph. It is generally a polynomial function whose degree is utmost 1 or 0. Although the linear functions are also represented in terms of calculus as well as linear algebra. The only difference is the function notation. Knowing an ordered pair written in function notation is necessary too. f(a) is called a function, where a is an independent variable in which the function is dependent. Linear Function Graph has a straight line whose expression or formula is given by;
y = f(x) = px + q
It has one independent and one dependent variable. The independent variable is x and the dependent one is y. P is the constant term or the y-intercept and is also the value of the dependent variable. When x = 0, q is the coefficient of the independent variable known as slope which gives the rate of change of the dependent variable.
What is a Nonlinear Function?
A function which is not linear is called nonlinear function. In other words, a function which does not form a straight line in a graph. The examples of such functions are exponential function, parabolic function, inverse functions, quadratic function, etc. All these functions do not satisfy the linear equation y = m x + c. The expression for all these functions is different.
Linear Function Graph
Graphing a linear equation involves three simple steps:
- Firstly, we need to find the two points which satisfy the equation, y = px+q.
- Now plot these points in the graph or X-Y plane.
- Join the two points in the plane with the help of a straight line.
Linear Function Table
See the below table where the notation of the ordered pair is generalised in normal form and function form.
| A normal ordered pair | A function notation ordered pair |
| (a,b) = (2,5) | f(a) = y coordinate, a=2 and y = 5, f(2) = 5 |
Using the table, we can verify the linear function, by examining the values of x and y. For the linear function, the rate of change of y with respect the variable x remains constant. Then, the rate of change is called the slope.
Let us consider the given table,
| x | y |
| 0 | 3 |
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
| 4 | 7 |
Form the table, it is observed that, the rate of change between x and y is 3. This can be written using the linear function y= x+3.
Linear Function Formula
The expression for the linear function is the formula to graph a straight line. The expression for the linear equation is;
y = mx + c
where m is the slope, c is the intercept and (x,y) are the coordinates. This formula is also called slope formula.
While in terms of function, we can express the above expression as;
f(x) = a x + b, where x is the independent variable.
Linear Function Characteristics
Let’s move on to see how we can use function notation to graph 2 points on the grid.
- Relation: It is a group of ordered pairs.
- Variable: A symbol that shows a quantity in a math expression.
- Linear function: If each term is either a constant or It is the product of a constant and also (the first power of) a single variable, then it is called as an algebraic equation.
- Function: A function is a relation between a set of inputs and a set of permissible outputs. It has a property that each input is related to exactly one output.
- Steepness: The rate at which a function deviates from a reference
- Direction: Increasing, decreasing, horizontal or vertical.
Linear Function Example
Graphing of linear functions needs to learn linear equations in two variables.
Example:
Find an equation of the linear function given f(2) = 5 and f(6) = 3.
Solution: Let’s write it in an ordered pairs
f(2) = 5, and f(6) = 3
(2, 5) (6, 3)
Find the slope.
(2, 5) (6, 3)
Slope = -1/2
In the equation, substitute the slope and y intercept , write an equation like this: y = mx+c
5 = -(½) (2) + b
5 = -1 + b
b = 5 + 1
b = 6, which is a y-intercept.
y = mx+b
y = -(½) (x) + 6
In function Notation: f(x) = -(½) (x) + 6
Visit BYJU’S to continue studying more on interesting Mathematical topics.



Comments