Number System Conversion Questions

The number system conversion questions and answers presented here will undoubtedly aid students in gaining a better understanding of the concept. Computer technology is one of the most important applications of the number system. The binary number system is used by computers, while people prefer the hexadecimal number system since it is easier to understand. As a result, a number system conversion is necessary. Several questions about number system conversion appear on practically every board exam. Students can use these questions to acquire a quick overview of the topics and practise them in order to gain a better knowledge of the subject. You can also check your answer against the answer on our page.

To completely grasp the idea, practice the number system conversion questions and solutions provided below.

Number System Conversion Questions with Solutions

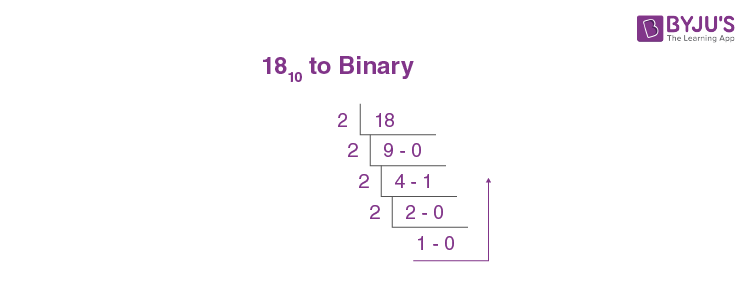
1. Convert the number 18₁₀ to the binary system.

Solution:

Given: 18₁₀.

Now, we have to convert the decimal system to the binary number system. Hence, the desired number’s base is 2.

Step 1: Divide 18 by 2, we get: quotient = 9 and remainder = 0

Step 2: Divide 9 by 2, we get: quotient = 4 and remainder = 1

Step 3: Divide 4 by 2, we get: quotient = 2 and remainder = 0

Step 4: Divide 2 by 2, we get: quotient = 1 and remainder = 0

Now, write the quotient obtained in step 4 the remainder from step 4 to step 1.

Hence, the binary equivalent of 18₁₀ is 10010₂.

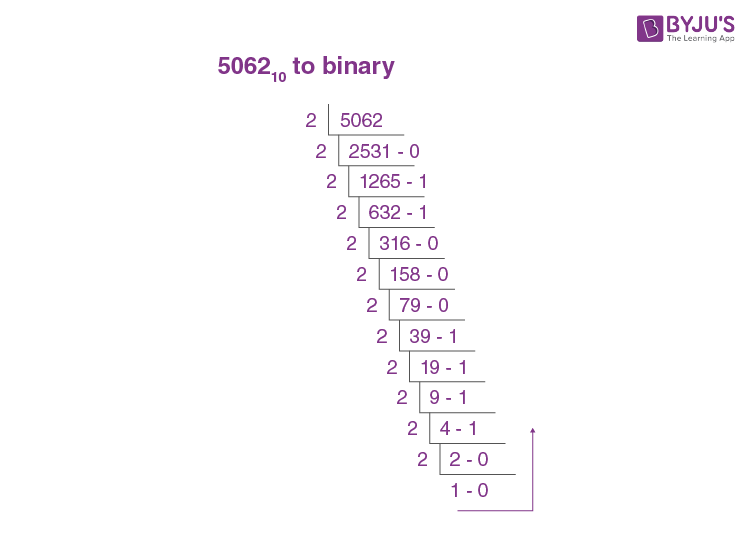
2. Convert the number 5062₁₀ to the binary system.

Solution:

Given: 5062₁₀.

Now, we have to convert the decimal system to the binary number system. Hence, the desired number’s base is 2.

Step 1: Divide 5062 by 2.

⇒ Quotient = 2531 & Remainder = 0

Step 2: Divide 2531 by 2.

⇒ Quotient = 1265 & Remainder = 1

Step 3: Divide 1265 by 2.

⇒ Quotient = 632 & Remainder = 1

Step 4: Divide 632 by 2.

⇒ Quotient = 316 & Remainder = 0

Step 5: Divide 316 by 2.

⇒ Quotient = 158 & Remainder = 0

Step 6: Divide 158 by 2.

⇒ Quotient = 79 & Remainder = 0

Step7: Divide 79 by 2.

⇒ Quotient = 39 & Remainder = 1

Step 8: Divide 39 by 2.

⇒ Quotient = 19 & Remainder = 1

Step 9: Divide 19 by 2.

⇒ Quotient = 9 & Remainder = 1

Step 10: Divide 9 by 2.

⇒ Quotient = 4 & Remainder = 1

Step 11: Divide 4 by 2.

⇒ Quotient = 2 & Remainder = 0

Step 12: Divide 2 by 2.

⇒ Quotient = 1 & Remainder = 0

To get the equivalent binary number for the decimal representation 5062₁₀, write the quotient obtained in step 12 and the remainder from step 12 to step 1.

Therefore, 5062₁₀ = 1001111000110₂.

3. Convert 159₁₀ to the octal number system.

Solution:

Given: 159₁₀

Here, the required base number is 8. (i.e., octal number system). Hence, follow the below procedure to convert the decimal system to the octal system.

Step 1: Divide 159 by 8.

⇒ Quotient = 19 & Remainder = 7

Step 2: Divide 19 by 8.

⇒ Quotient = 2 & Remainder = 3

Since, the quotient “2” is less than “8”, we can stop the process.

Therefore, 159₁₀ = 237₈

4. Convert 380₁₀ to the hexadecimal number system.

Solution:

Given: 380₁₀

Now, we have to convert the decimal system to the hexadecimal number system.

So, divide the given number by 16.

Step 1: Divide 380 by 16.

⇒ Quotient = 23 & Remainder = 12 (12 can be represented as “C” in the hexadecimal number system)

Step 2: Divide 23 by 16.

⇒ Quotient = 1 & Remainder = 7

As the quotient 1 is less than 16, stop the process.

Hence, 380₁₀ = 17C₁₆.

5. Convert the binary number 11001011₂ to the decimal number system.

Solution:

Given binary number: 11001011₂

Now, multiply each digit of the given binary number by the exponents of the base, starting with the right to left such that the exponents start with 0 and increase by 1.

Hence, the digits from right to left are written as follows:

1 = 1 × 2⁰ = 1

1 = 1 × 2¹ = 2

0 = 0 × 2² = 0

1 = 1 × 2³ = 8

0 = 0 × 2⁴ = 0

0 = 0 × 2⁵ = 0

1 = 1 × 2⁶ = 64

1 = 1 × 2⁷ = 128

Now, add all the product values obtained.

= 1 + 2 + 0+ 8 + 0 + 0 + 64 + 128

= 203

Hence, the decimal equivalent of 11001011₂ is 203₁₀.

I.e., 11001011₂ = 203₁₀.

Alternate Method:

11001011₂ = (1 × 2⁷) + (1 × 2⁶) + (0 × 2⁵) + (0 × 2⁴) + (1 × 2³ ) + (0 × 2²) + (1 × 2¹ ) + (1 × 2⁰ )

11001011₂ = 128 + 64 + 0 + 0 + 8 + 0 + 2 + 1

11001011₂ = 203₁₀.

6. Convert the octal number 714₈ to the decimal number.

Solution:

Given octal number: 714₈

Since the base of the octal number system is 8, we have to multiply each digit of the given number with the exponents of the base.

Thus, the octal number 714₈ can be converted to the decimal system as follows:

714₈ = (7 × 8²) + (1 × 8¹) + (4 × 8⁰)

714₈ = (7 × 64) + ( 1 × 8) + (4 × 1)

714₈ = 448 + 8 + 4

714₈ = 460₁₀

Hence, the decimal equivalent of the octal number 714₈ is 460₁₀.

7. Convert 11101₂ to the decimal number system.

Solution:

Given binary number: 11101₂

Now, multiply each digit of 11101 with the exponents of the base, such that the exponents start with 0, and increase by 1 when moving from right to left.

So, 11101₂ = (1 × 2⁴) + (1 × 2³ ) + (1 × 2²) + (0 × 2¹ ) + (1 × 2⁰ )

11101₂ = 16 + 8 + 4 + 0 + 1

11101₂ = 29₁₀

Hence, the decimal number system 29₁₀ is equivalent to the binary number system 11101₂.

8. Convert the hexadecimal number 2C4 to the decimal number system.

Solution:

Given hexadecimal number is 2C4.

As we know, the base of the hexadecimal number is 2C4.

Thus, 2C4 in the decimal number system is given as follows:

2C4₁₆ = (2 × 16²) + (12 × 16¹) + (4 × 16⁰)

2C4₁₆ = (2 × 256) + (12 × 16) + (4 × 1)

2C4₁₆ = 512 + 192 + 4

2C4₁₆ = 708₁₀

Hence, the hexadecimal number 2C4₁₆ is equivalent to 708₁₀.

9. Convert 1001₂ to octal number system.

Solution:

Given: 1001₂.

To convert the binary number system to the octal number system, first we have to convert the binary system into decimal system, and then convert the decimal system to the octal number.

Conversion from Binary System to the Decimal System:

1001₂ = (1 × 2³) + (0 × 2²) + (0 × 2¹) + (1 × 2⁰)

1001₂ = (1 × 8) + (0 × 4) + (0 × 2) + (1 × 1)

1001₂ = 8 + 0 + 0 + 1

1001₂ = 9₁₀

Conversion from Decimal Number System to the Octal Number System:

Here, we have to convert 9₁₀ to the octal system, and the required base is 8.

Hence,

Step 1: Divide 9 by 8.

⇒ Quotient = 1 & Remainder = 1

Since, quotient “1” is less than “8”, we cannot proceed further.

Therefore, the octal equivalent of 9₁₀ is 11₈

Hence, the octal number system equivalent to 1001₂ is 11₈.

10. Convert 672₈ to the hexadecimal number system.

Solution: decimal= 442, hexa = 1BA

Given: 672₈ (i.e., octal number system)

Conversion from Octal to Decimal Number System:

The conversion from the octal number system to the decimal system is as follows:

672₈ = (6 × 8²) + (7 × 8¹) + (2 × 8⁰)

672₈ = (6 × 64) + (7 × 8) + (2 × 1)

672₈ = 384 + 56 + 2

672₈ = 442₁₀

Conversion from Decimal to the Hexadecimal Number System:

Now, the number in the decimal system is 442₁₀.

Thus, the process of converting the decimal number system to the hexadecimal system is as follows:

Step 1: Divide 442 by 16

⇒ Quotient = 27 & Remainder = 10 (Number 10 in hexadecimal system is A)

Step 2: Divide 27 by 16

⇒ Quotient = 1 & Remainder = 11 (Number 11 in hexadecimal system is B)

So, 442₁₀ = 1BA₁₆

Therefore, the octal number 672₈ equivalent to the hexadecimal number system is 1BA₁₆.

Explore More Articles

• Perimeter and Area Questions
• Arithmetic Questions
• BODMAS Rule Questions
• Functions Questions
• Decimal to Binary Questions
• Conditional probability Questions

Practice Questions

Solve the following number system conversion questions:

1. Convert 489₁₀ to binary number system.
2. Convert 4BC to the decimal number system.
3. Convert 546₈ to the hexadecimal number system.

Download BYJU’S – The Learning App to learn all Maths-related topics by exploring more interesting videos.