Before going to the definition of an equation, let’s understand how an equation works and how to identify the pattern that makes an equation. This can be understood with the help of the below scenario. Consider the pattern of triangles formed by matchsticks in the figure given below:

Using the above pattern, find the general rule that gives the number of triangles formed by 95 matchsticks.
We may observe that the number of matchsticks in the given matchstick pattern is 3, 5, 7, 9 and so on.
That means the 1st triangle is formed by 3 matchsticks, and the 2nd triangle is formed by adding 2 more sticks to the first one.
Similarly, the third triangle is formed by adding another 2 matchsticks to the previous pattern.
Thus,
| Number of triangles | Number of matchsticks |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
From this, we can say that there is 1 more than twice the number of triangles in the pattern.
Let us take “x” as a variable to form the equation.
Here, the pattern is 2x + 1, where x is the number of triangles.
Now, we can find the number of triangles formed by 95 matchsticks as:
2x + 1 = 95
2x = 94
x = 94/2
x = 47
Hence, we can form 47 triangles using 95 matchsticks in the given pattern.
In the above example, 2x + 1 = 95 represents the equation.
| Read more: |
Equation meaning
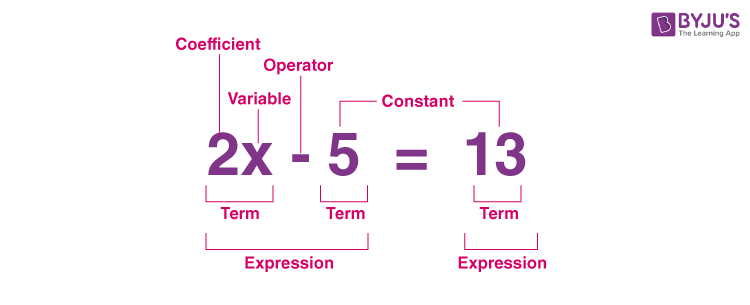
Mathematically, an equation can be defined as a statement that supports the equality of two expressions, which are connected by the equals sign “=”. For example, 2x – 5 = 13.
Here,
2x – 5 and 13 are expressions
The sign that connects these two expressions is “=”.
Parts of Equation
The parts of the equation 2x – 5 = 13 are explained below.
An equation combines two expressions connected by an equal sign (“=”). These two expressions on either side of the equals sign are called the “left-hand side” and “right-hand side” of the equation. We generally assume the right-hand side of an equation is zero. This will not reduce the generality since we can balance this by subtracting the right-hand side expression from both sides’ expressions.
Equation algebra
In algebra, an equation is a condition on a variable. It is satisfied only for a definite value of the variable. That means, the equation 2x – 5 = 13 is satisfied only for x = 9.
The below figure shows the difference between expression and equation in algebra.

Equation Types
Algebra considers two prominent families of equations, namely polynomial equations and linear equations. Polynomial equations with one variable can be written in P(x) = 0, where P is a polynomial, and ax + b = 0 is the general form of linear equations. Here, a and b are parameters. We can practice geometric or algorithmic methods from linear algebra or mathematical analysis to solve these equations. Also, there are different types of equations, such as:
- Linear equations
- Quadratic equations
- Cubic equations
- Quartic equations
- Differential equations
- Parametric equations
Equation of a line
The standard form of the equation of a line is Ax + By + C = 0. The slope-intercept form of an equation is y = mx + b, where m is the slope of the line and b is the y-intercept. However, there are various types of equations to represent lines.
Click here to know more about the different types of equations of lines.
Equation of x-axis
Generally, we say that the equation of the x-axis equation is of the form y = 0. However, we can also write the x-axis equation as x = c where c is constant.
The x-axis comprises all the real values of x, although the value of y is equal to 0 on the complete x-axis.
Thus, x can be recognised as constant and y as 0.
In the coordinate system representation, we can represent any point on the x-axis as (c, 0), where c is any real number.
Therefore, the x-axis formula will be x= c + y
Here,
c = constant
y = 0
The x-axis formula is x = c, where c is constant.
Equation in One Variable
The equation in one variable means the equation containing only one variable. Let’s have a look at the below equations.
17 – 9 = 8
x + 4 = 4y + 22z
4x2 + 3x – 7 = 0
The three examples above represent equations that propose equality (could be true or not) between two expressions.
The first equation does not contain any variable.
The second equation has three different variables, such as x, y and z. Thus, it is a multivariate equation.
The third equation contains only one variable, i.e. x. Thus, this is an equation in one variable.
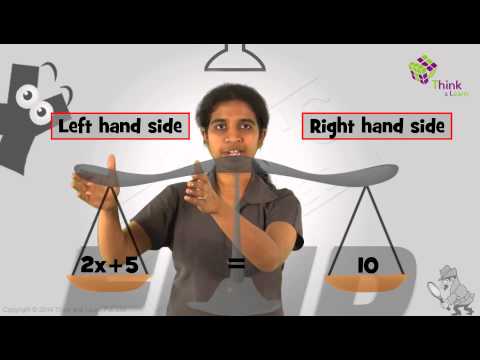
Watch the Below Video Lesson to Know how to Solve an Equation
Equation Examples
Go through the examples of equations and their solutions given below.
Example 1:
Identify the variable and the value of the variable that satisfy the given equation for the following:
(a) 5b = 60
(b) x + 12 = 20
(c) m – 5 = 5
(d) p/2 = 7
Solution:
(a) 5b = 60
b = 60/5
b = 12
Therefore, the variable is “b” and the solution is b = 12.
Alternative method:
5b = 60
Dividing both sides of the equation by 5,
5b/5 = 60/5
b = 12
(b) x + 12 = 20
x = 20 – 12
x = 8
Here, the variable is “x” and the solution is x = 8.
Alternatively,
x + 12 = 20
Subtracting 12 from both sides of the equation,
x + 12 – 12 = 20 – 12
x = 8
(c) m – 15 = 25
m = 25 + 15
m = 40
Here, the variable is “m” and the solution is m = 40.
Alternative method:
m – 15 = 25
Adding 15 on both sides,
m -15 + 15 = 25+ 15
m = 40
(d) p/2 = 7
p = 2 × 7
p = 14
Here, the variable is “p” and the solution is p = 14.
Alternative method:
p/2 = 7
Multiplying 2 on both sides of the equation,
(p/2) × 2 = 7 × 2
p = 14
Example 2:
Solve the equation: 6(2x + 3) + x – 7 = 3(5x + 7) + 2x
Solution:
6(2x + 3) + x – 7 = 3(5x + 7) + 2x
Expanding the terms we get,
12x + 18 + x – 7 = 15x + 21 + 2x
13x + 11 = 17x + 21
On further simplification,
13x – 17x = 21 – 11
-4x = 10
x = -10/4
x = -5/2
Frequently Asked Questions on Equation
Define an equation with an example.
For example, 3x – 5 = 16 is an equation. Solving this equation, we get the value of the variable x as x = 7.
What are the types of equations?
Linear equations
Quadratic equations
Cubic equation
Quartic equations
Differential equations
Parametric equations

Comments