Exponential growth increases without bound. This is possible for some situations like population, where there is usually some type of upper bound. This leads to limitations on food, space or other scarce resources. Logistic growth is a type of growth where the effect of limiting upper bound is a curve that grows exponentially at first and then slows down and hardly grows at all.
Definition:
A function that models the exponential growth of a population but also considers factors like the carrying capacity of land and so on is called the logistic function. It should be remembered that the logistic function has an inflection point.
Pierre Francois Verhulst introduced the logistic function.
Read more:
Logistic Function Equation
The standard logistic function is a logistic function with parameters k = 1, x0 = 0, L = 1.
This reduces the logistic function as below:

Logistic curve

The equation of logistic function or logistic curve is a common “S” shaped curve defined by the below equation. The logistic curve is also known as the sigmoid curve.

Where,
L = the maximum value of the curve
e = the natural logarithm base (or Euler’s number)
x0 = the x-value of the sigmoid’s midpoint
k = steepness of the curve or the logistic growth rate
The exponential function in the denominator completely determines the rate at which a logistic function falls from or rises to its limiting value.
Note:
Carrying capacity is the population limit or the maximum population that the environment can support.
Derivative of the logistic function

This derivative is also known as logistic distribution.
Integral of the logistic function
Assume 1+ex = u
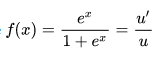

Logistic Function Examples
Spreading rumours and disease in a limited population and the growth of bacteria or human population when resources are limited.
There are many applications where logistic function plays an important role. Some of them are as follows.
Ecology: Modeling population growth, time-varying carrying capacity.
Statistics and machine learning: logistic regression and neural networks
Medicine: Modeling of growth of tumours
Agriculture: Modeling crop response
Example problem 1:
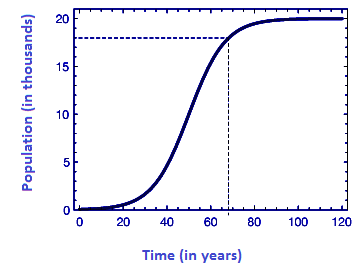
How many years will it take for a bacteria population to reach 9000, if its growth is modelled by
 here, t in years?
here, t in years?
Solution:
According to the given,

Taking logarithm on both sides,
-0.12(t-20)=ln(0.111)
t = -ln(0.111)/0.12 + 20
On simplifying,
t=38.31 years
The graph for the above solution is as below:
Logistic function vs Sigmoid function
A mathematical function which is having S-shaped curve or a sigmoid curve is called sigmoid function. When a standard choice has been added for a sigmoid function is considered as the logistic function. Sigmoid function has a domain of all real numbers, with return value strictly increasing from 0 to 1 or alternatively from −1 to 1, depending on convention.

Comments