Arithmetic Mean in Statistics

The measures of central tendency enable us to make a statistical summary of the enormous organized data. One such method of measure of central tendency in statistics is the arithmetic mean. This condensation of a large amount of data into a single value is known as measures of central tendency.

For example, in the early morning while reading a newspaper, have you observed the daily temperature reports. Well, the temperature varies all day still how a single temperature can indicate the condition for the entire day? Or when you get your scorecard in exams, instead of analyzing your performance based on the percentage in all subjects, the performance is based upon the aggregate percentage.

The significance of indicating a single value for a large amount of data in real life makes it easy to study and analyze the collection of data and deduce important information out of it. Let us discuss the arithmetic mean in Statistics and examples in detail.

What is Arithmetic Mean in Statistics?

The most common measure of central tendency is the arithmetic mean. In layman’s terms, the mean of data indicates an average of the given collection of data.  It is equal to the sum of all the values in the group of data divided by the total number of values.

For n values in a set of data namely as x₁, x_2, x_{3, …} x_n, the mean of data is given as:

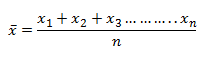
It can also be denoted as:

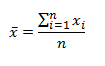
For calculating the mean when the frequency of the observations is given, such that x₁, x_2, x_3,… x_n is the recorded observations, and f₁, f_2, f₃ … f_n is the respective frequencies of the observations then;

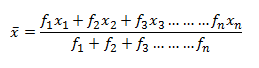
This can be expressed briefly as:

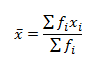
The above method of calculating the arithmetic mean is used when the data is ungrouped in nature. For calculating the mean of grouped data, we calculate the class mark.  For this, the midpoints of the class intervals are calculated as:

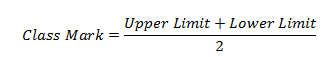
After calculating the class mark, the mean is calculated as discussed earlier. This method of calculating the mean is known as the direct method.

Mean Definition in Statistics

As we have understood about the arithmetic mean, now let us understand what does the mean stands for in statistics.

Mean is nothing but the average of the given values in a data set.

Mean = Sum of given values/Total number of values

Majorly the mean is defined for the average of the sample, whereas the average represents the sum of all the values divided by the number of values. But logically both mean and average is same.

For example, find the mean of given values: 2,3,4,5,6,6,

Mean = (2+3+4+5+6+6)/6 = 26/6 = 13/3

Examples of Arithmetic Mean in Statistics

Let us look into an example to understand this clearly.

Example 1: 

In a class of 30 students, marks obtained by students in mathematics out of 50 is tabulated below. Calculate the mean of the data.

Solution:

The mean of the data given above is,

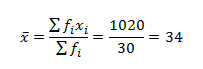
Thus, the mean of the given data is 34.

Example 2: 

Calculate the arithmetic mean of the first 7 natural numbers.

Solution:

We know that the first 7 natural numbers are 1, 2, 3, 4, 5, 6, 7.

We know that,

Arithmetic Mean = Sum of all values / Total number of values.

Hence, the arithmetic mean of first 7 natural numbers = Sum of first 7 natural numbers/Total number of natural numbers.

Arithmetic Mean = (1+2+3+4+5+6+7)/7

AM = 28/7

AM = 4

Therefore, the arithmetic mean of the first 7 natural numbers is 4.

Example 3:

Determine the mean of the first 5 prime numbers.

Solution:

The first 5 prime numbers are 2, 3, 5, 7 and 11.

Hence, the mean of the first 5 prime numbers is calculated as follows:

Mean = Sum of first 5 prime numbers/Total number of prime numbers

Mean = (2+3+5+7+11)/5

Mean = 28/5 = 5.6.

Therefore, the mean of the first 5 prime numbers is 5.6.

To know more about measures of central tendency and arithmetic mean, please download BYJU’S – The Learning App and stay tuned with us.