In Maths, a variable is an alphabet or term that represents an unknown number or unknown value or unknown quantity. The variables are specially used in the case of algebraic expression or algebra. For example, x+9=4 is a linear equation where x is a variable, where 9 and 4 are constants.
The variable is a quantity that can be changed or which is not fixed according to the mathematical operation performed. Usually, in algebra, we express an unknown number using the term ‘x’ and ‘y’. But this is not particular, and we can use any alphabet.
Learn more: Variables And Constants In Algebraic Expressions
In this article, we are going to discuss what is a variable in Math, types of variables such as dependent variable and independent variable with examples.
Table of contents:
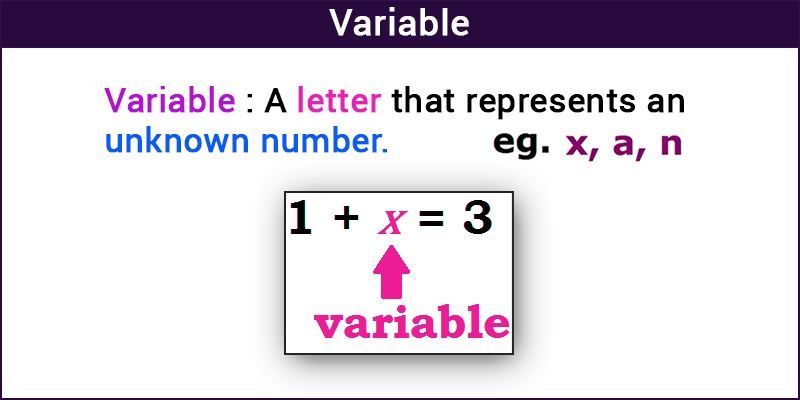
Definition
A variable in Mathematics is defined as the alphabetic character that expresses a numerical value or a number. In algebraic equations, a variable is used to represent an unknown quantity.
These variables can be any alphabets from a to z. Most commonly, ‘a’,’b’,’c’, ‘x’,’y’ and ‘z’ are used as variables in equations.
Making arithmetical calculations with variables as though they were express numbers permits one to take care of scope of issues in a solitary calculation. An ordinary illustration is a quadratic recipe, which allows one to explain each quadratic condition by just substituting the numerical estimations of the coefficients of the offered condition to the variables that speak to them.
The idea of a variable is significant in math. Regularly, a function y = f(x) includes two variables, y and x, speaking to individually the quality and the contention of the function. The expression “variable” originates from the way that when the argument (additionally called the “variable of the capacity”) shifts, then the quality changes accordingly.
Parts of Equation
The equations in Mathematics are formed of different parts. They are:
For example, in equation, 3x+9 = 21,
x → Variable
3 → coefficient of x
9 and 21 → constants
‘+’ → operator
Operator: An operator is an arithmetic symbol that is used to perform various operations on the values. These operators are (+, -, ×, ÷, etc.).
Term: A term is a single expression of an equation. It can be a number or a variable or a number multiplied by a variable.
Examples of Variables
- x+2=8
- y+3=12
- 5x-2=10
- 4x/3=7
In the above examples, x and y are called variables.
Constant in Math
The constants in math are the values which cannot be changed or which are fixed. It is a contradiction to the variable. In algebraic expressions, the constant are terms which define themselves.
For example, if 9x+2=15 is an equation, then;
x is the variable, which can have different values and 9 is the coefficient of x.
But numbers 2 and 15 are the constant here.
Variable in Statistics
In statistics, the variables are used in terms of real-life scenarios. It is also said to be an attribute here. They are used to representing people, places, things, etc. For example, the colour of the hair of a person is a variable. Since the hair-colour could vary from person to person like for some it is blond, for some, it is black, etc.
Types of variables in Math
The variables can be classified into two categories, namely
- Dependent Variable
- Independent Variable
Let’s discuss the two types of variables in detail.
Dependent Variables
The dependent variable is characterized as the variable whose quality depends on the estimation of another variable in its condition. That is, the estimation of the word variable is dependably said to be reliant on the free variable of math condition.
For instance, consider the condition y = 4x + 3. In this condition, the estimation of the variable ‘y’ changes as per the adjustments in the estimation of ‘x’. In this manner, the variable ‘y’ is said to be a reliant variable. A portion of the cases that include subordinate variables is talked about in point of interest as beneath with their answers.
Independent Variables
In an algebraic equation, an independent variable describes a variable whose values are independent of changes. If x and y are two variables in an algebraic equation and every value of x is linked with any other value of y, then ‘y’ value is said to be a function of x value known as an independent variable, and ‘y’ value is known as a dependent variable.
Example: In the expression y = x2, x is an independent variable and y is a dependent variable.
Thus, we can summarise the variables mathematically as given below:
In mathematics, we can define variables with the help of a function; In simple words, a function is a rule for taking a number or set of numbers as input and producing an output which may also be a number or set of numbers. The most common character used to denote the input is x, and the result is y. Thus, the function is written in the form of y = f(x). Here, the character that stands for a random input is called an independent variable, i.e. x, whereas a symbol that stands for an arbitrary output is called a dependent variable; in this case, it is y.
Apart from these dependent and independent variables, there exist other types of variables such as:
- Random variables
- Categorical and continuous variables
- Intervening variables
- Moderator variables
- Control variables
- Extraneous variables
- Free variables
- Bound variables
Application of Variables
Variables are not used in the field of Mathematics but also in various other fields for different purposes, such as:
For a better understanding of the concepts, register with BYJU’S – The Learning App and watch the interactive videos to learn with ease.


Comments