A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the centre of base) called the apex or vertex. We can also define the cone as a pyramid which has a circular cross-section, unlike pyramid which has a triangular cross-section. These cones are also stated as a circular cone.
Definition of Cone
A cone is a shape formed by using a set of line segments or the lines which connects a common point, called the apex or vertex, to all the points of a circular base(which does not contain the apex). The distance from the vertex of the cone to the base is the height of the cone. The circular base has measured value of radius. And the length of the cone from apex to any point on the circumference of the base is the slant height. Based on these quantities, there are formulas derived for surface area and volume of the cone. In the figure you will see, the cone which is defined by its height, the radius of its base and slant height.
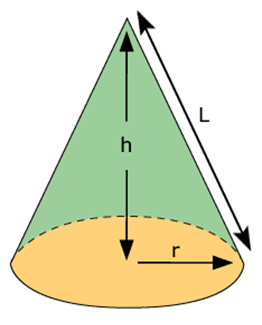
Cone
Also, read:
Cone Formula – Slant Height, Surface Area of Cone & Volume of Cone
The formula for the surface area and volume of the cone is derived here based on its height(h), radius(r) and slant height(l).
Slant Height
The slant height of the cone (specifically right circular) is the distance from the vertex or apex to the point on the outer line of the circular base of the cone. The formula for slant height can be derived by the Pythagoras Theorem.
Slant Height, l = √(r2+h2)
Volume of the Cone
We can write, the volume of the cone(V) which has a radius of its circular base as “r”, height from the vertex to the base as “h”, and length of the edge of the cone is “l”.
Volume(V) = ⅓ πr2h cubic units
Surface Area of the Cone
The surface area of a right circular cone is equal to the sum of its lateral surface area(πrl) and surface area of the circular base(πr2). Therefore,
The total surface area of the cone = πrl + πr2
Or
Area = πr(l + r)
We can put the value of slant height and calculate the area of the cone.
Types of Cone
As we have already discussed a brief definition of the cone, let’s talk about its types now. Basically, there are two types of cones;
- Right Circular Cone
- Oblique Cone
Right Circular Cone
A cone which has a circular base and the axis from the vertex of the cone towards the base passes through the center of the circular base. The vertex of the cone lies just above the center of the circular base. The word “right” is used here because the axis forms a right angle with the base of the cone or is perpendicular to the base. This is the most common types of cones which are used in geometry. See the figure below which is an example of a right circular cone.
Oblique Cone
A cone which has a circular base but the axis of the cone is not perpendicular with the base, is called an Oblique cone. The vertex of this cone is not located directly above the centre of the circular base. Therefore, this cone looks like a slanted cone or tilted cone.

Properties of Cone
- A cone has only one face, which is the circular base but no edges
- A cone has only one apex or vertex point.
- The volume of the cone is ⅓ πr2h.
- The total surface area of the cone is πr(l + r)
- The slant height of the cone is √(r2+h2)
Frustum of Right Circular Cone
Frustum of a cone is a piece of the given circular or right circular cone, which is cut in a manner that the base of the solid and the plane cutting the solid are parallel to each other. Based on this, we can calculate the surface area and volume also. For more details, read the frustum of a cone from here.
Examples
Question: Find the volume of the cone if radius, r = 4 cm and height, h = 7 cm.
Solution: By the formula of volume of the cone, we get,
V = ⅓ πr2h
V = (⅓) × (22/7) × 42 × 7
V = 117.33 Cubic Cm
Question: What is the total surface area of the cone with the radius = 3 cm and height = 5 cm?
Solution: By the formula of the surface area of the cone, we know,
Area = πr(l + r)
Since, slant height l = √(r2+h2) = √(32+52) = √(9+25) = √34
Therefore,
Area, A = π × 3(√34 + 3) = π × 3(5.83 + 3) = π × 3(8.83) = 83.22 Cm2
Related Links:
| Pyramid | Circles |
| Triangles | Square |
| Cube | Cylinder |
Download BYJU’S – The Learning App and get personalised video content based on different geometrical concepts of Maths.


Comments