
The environment is incomplete without microorganisms. With every breath you take, there are millions of microscopic organisms that you breathe in. Apart from that, the human body hosts a plethora of microbes both inside and outside. Besides this, they are a crucial part of the ecosystem and take part in activities like production of minerals like nitrogen, gases like oxygen, carbon dioxide, taking care of dead and decaying materials etc.

What are Microorganisms?
Microorganisms are small, living creatures which are invisible to our naked eye. Hence, they are also known as microorganisms or microscopic organisms. These organisms can be unicellular or multicellular. Among all microorganisms, some are harmful and disease-causing pathogens, while others include useful microbes, which are more beneficial and harmless to humans.
Also Read: Types of Microbes
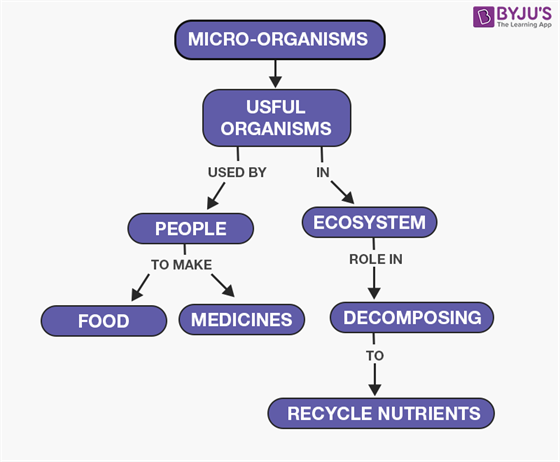
Uses of Microorganisms
As discussed, microorganisms are beneficial for humans in various ways. They play an important role in human welfare and for the environment. These include processing and preservation of food, production of biomolecules, manufacture of pharmaceutical products, cosmetics industries, recycling the nutrients in the soil and so on. Listed below are some of the applications of microorganisms in human welfare.
Food Industry and Beverages
The role of microorganisms in food preparation and beverage manufacturing is known for ages. They are used in the manufacture of bread, curd, wine, and alcohol etc. Lactobacillus bacteria are responsible for the curd formation. They multiply and convert milk into curd. Another example is Yeast which is used commercially for alcohol and wine production. The process is called fermentation. Yeast is also used in baking industries for the preparations of bread and cakes.
Also Read: Food production
Micro-flora
Bacteria are not only present outside the human body, but they also live inside the body too. This aggregate collection of microorganisms that is present in the human body is termed as Microflora.
Bacteria are also present in the gut, and they aid the process of digestion by releasing certain enzymes. They live in a symbiotic relationship with a human. Other roles of microflora are vitamin K production, which is crucial in enabling blood clotting. They also prevent the invasion of the foreign bodies, by acting against other fatal microbes.
Also Read: Bacteria
Pharmaceutical Industry
Antibiotics go hand in hand with microbes in the medical field. Typically, antibiotics are obtained from a weakened form of an otherwise harmful microorganism. This is then injected into the body and the body learns to fight off the diseases caused by these organisms. Examples of this include mumps and the measles.
Environment
In the environment, microorganisms have two vital roles- one is an enhancement of soil fertility another is cleaning. Azotobacter, Rhizobium, Clostridium are few examples of Nitrogen-fixing bacteria which play a primary role in transforming atmospheric nitrogen into inorganic compounds which are then used by the plants. Without this process, the vast majority of the nitrogen present in the atmosphere becomes unusable.
Microorganisms also act as cleaners. Plants and animals eventually die and their bodies are turned into nutrients which the environment can use.
Also Read: Our environment
For more instances of useful microorganisms and other related topics, visit BYJU’S Biology.
Frequently Asked Questions
What are useful microorganisms?
Name a few useful microorganisms.
Following are a few useful microorganisms:
- Bacteria
- Fungi
- Protozoa

useful
Ma’am, in uses of microorganisms, under pharmaceutical industry, I think, the description given for antibiotics actually fits for a vaccine. Please check the content.
Antibiotics and vaccines are similar in a way that they are injected into the body as both possess antimicrobial properties to treat infections. But they possess many dissimilarities. One such differentiating factor is that antibiotics are administered after a person is infected while vaccines, in most cases, serve as a preventive measure, administered in advance prior to the manifestation of infection.
Byjus is a useful app
Interactive teaching and amazing knowledge about the subject.
Wonderful excellent.