Kerala Plus Two Maths Previous Question Papers and Answers 2017 In PDF

Kerala Class 12th Maths Question Paper 2017 Solved – Free Download

Kerala Plus two (Class 12) maths 2017 question paper with answers are provided here in a downloadable pdf format and also in the text, so that the students can avail them easily. Along with the solutions, maths question paper 2017 Plus Two is also added here for good practice. 12th Class Students are able to access all the Kerala board previous year maths question papers. The solutions provided by BYJU’S will assist the students in understanding the concepts clearly. Solving 2017 Maths question papers and also the previous year papers for Class 12 will equip the students to ace the exam as mathematics is a subject which requires a lot of practice.

Question 1[a]: Let R be a relation defined on A = {1, 2, 3} by R = [{1, 3} , {3, 1}, {2, 2}]. R is

(a) Reflexive (b) Symmetric

(c) Transitive (d) Reflexive but not transitive

Answer: [b]

[b] Find f o g and g o f if f(x) = |x + 1| and g (x) = 2x – 1.

Solution:

f o g (x) = f (g (x)) = f (2x – 1)

= |2x – 1 + 1|

= |2x|

g o f (x) = g (f (x)) = g (x + 1)

= 2 |x + 1| – 1

[c] Let “*” be a binary operation defined on N x N by (a, b) * (c, d) = (a + c, b + d). Find the identity element for * if it exists.

Solution:

If (c, d) is the identity element,

(a, b) * (c, d) = (a, b)

(a, b) * (c, d) = (a + c, b + d)

(a + c, b + d) = (a, b)

(c, d) = (0, 0) is not an element of N x N.

So, the identity element doesn’t exist.

Question 2[a]: The principal value of cot^-1 (1 / √3) is

(a) 𝛑 / 3 (b) – 𝛑 / 3 (c) 𝛑 / 6 (d) 2𝛑 / 3

Answer: [d]

[b] Solve tan^-1 (x – 1) / (x – 2) + tan^-1 (x + 1) / (x + 2) = 𝛑 / 4.

Solution:

tan^-1 (x – 1) / (x – 2) + tan^-1 (x + 1) / (x + 2)

𝛑 / 4 = tan^-1 [{(x – 1) / (x – 2)} + {(x + 1) / (x + 2)}] / [1 – {(x – 1) / (x – 2)} * {(x + 1) / (x + 2)}]

𝛑 / 4 = [2x² – 4] / -3

x = ± 1 / √2

Question 3[a]: The value of k such that the matrix 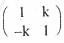is symmetric is

(a) 0 (b) 1 (c) -1 (d) 2

Answer: k = 0

[b] If A = 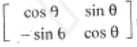then prove that A² = .

Solution:

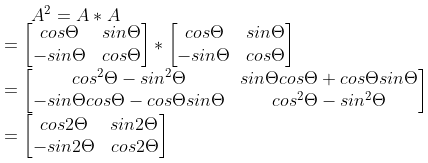
[c] If A = 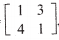, then find |3A’|.

Solution:

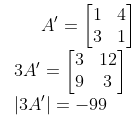
Question 4[a]: If A = 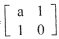such that A² = I then a equals to

(a) 1 (b) -1 (c) 0 (d) 2

Answer: [c]

[b] Solve the system of equations:

x – y + z = 4

2x + y – 3z = 0

x + y + z = 2 by matrix method.

Solution:

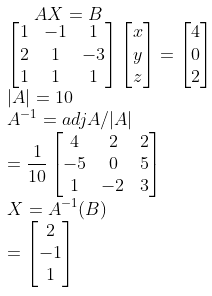
Question 5[a]: Find the value of a and b such that the function

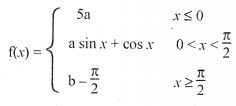
is continuous.

Solution:

5a = 1

a = 1 / 5

a = b – (𝛑 / 2)

b = (1 / 5) + (𝛑 / 2)

[b] Find dy / dx if (sin x)^{cos y} = (cos y)^{sin x}.

Solution:

log ((sin x)^{cos y}) = log (cos y)^{sin x}

cos y log sin x = sin x log cos y

cos y * ( 1 / sin x) * cos x + log sin x * (- sin y) (dy / dx) = sin x * (1 / cos y) * (- sin y) (dy / dx) log cos y cos x

dy / dx = [cos x * log cos y – cos y cot x] / [sin x tany – sin y log sin x]

Question 6[a]: Slope of the normal curve y² = 4x at (1, 2) is

(a) 1 (b) 1 / 2 (c) 2 (d) -1

[b] Find the interval in which 2x³ + 9x² + 12x – 1 is strictly increasing.

OR

[a] The rate of change of volume of a sphere with respect to its radius when its radius is 1 unit

(a) 4𝛑 (b) 2𝛑 (c) 𝛑 (d) 𝛑 / 2

[b] Find two positive numbers whose sum is 16 and the sum of whose cubes are minimum.

Solution:

f’ (x) = 0

x = -1, -2

The intervals are (- ∞, -2), (- 2, – 1) and (- 1, ∞).

f’ (x) > 0 is increasing in (- ∞, -2) and (- 1, ∞).

OR

x + y = 16

y = 16 – x

Sum S = x² + y²

= x² + (16 – x)²

= x² + 256 + x² – 32x

= 2x² – 32x + 256

dS / dx = 4x – 32

For the sum to be minimum, dS / dx = 0

4x – 32 = 0

4x = 32

x = 8

y = 16 – x

Substituting the x value,

y = 16 – 8 = 8

So, the two numbers are 8 and 8.

Question 7: Find the following.

[a] ∫1 / [x (x⁷ + 1)] dx

[b] ∫₁⁴ |x – 2| dx

Solution:

= ∫x⁶ / [x⁷ (x⁷ + 1)] dx

Put t = x⁷

dt = 7x⁶ dx

= (1 / 7) ∫dt / t (t + 1)

= (1 / 7) [∫([1 / t] + [-1 / t + 1])] dt

= (1 / 7) [log x⁷ – log (1 + x⁷)] + c

= ∫₁² (2 – x) dx + ∫₂⁴ (x – 2) dx

= [(2 – x)² / -2]₁² + [(x – 2)² / 2]₂⁴

= (0 – (-1 / 2)) + ((4 / 2) + 0)

= 5 / 2

Question 8[a]: Evaluate ∫₀^𝛑/2 log sin x dx

OR

[b] Evaluate ∫₀⁴ x² dx as the limit of a sum.

Solution:

= ∫₀^𝛑/2 log sin (𝛑 / 2 – x) dx

I = ∫₀^𝛑/2 log cos x dx

2I = ∫₀^𝛑/2 [log sin x + log cos x] dx

= ∫₀^𝛑/2 log sin 2x – ∫₀^𝛑/2 log 2 dx

= I – (𝛑 / 2) log 2

I = – (𝛑 / 2) log 2

= lim _h→0 h³ [1² + 2² + …… (n – 1)²]

= lim _h→0 h³ [n (n – 1) (2n – 1) / 6]

= lim _h→0 h³ n³ * (1 – [1 / n]) (2 – [1 / n]) / 6

= 4 * 4 * 8 / 6

= 64 / 3

Question 9[a]: Area bounded by the curves y = cos x, x = 𝛑 / 2, x = 0, y = 0 is

(a) 1 / 2 (b) 2 / 𝛑 (c) 1 (d) 𝛑 / 2

[b] Find the area between the curve y² = 4ax and x² = 4ay, a > 0.

Solution:

[a] Answer: (c)

The point of intersection is (4a, 4a).

Area = ∫₀^4a √4ax dx – ∫₀^4a (x² / 4a) dx

= 2√a [(x^3/2 / (3 / 2)]₀^4a – (1 / 4a) (x³ / 3)₀^4a

= [16 / 3] a²

Question 10[a]: The order of the differential equation x⁴ d²y / dx² = 1 + (dy / dx)³ is

(a) 1 (b) 3 (c) 4 (d) 2

[b] Find the particular solution of the differential equation (1 + x²) dy / dx + 2xy = 1 / 1 + x², y = 0 when x = 1.

Solution:

Divide both sides by (1 + x²)

dy / dx + 2xy / 1 + x² = 1 / (1 + x²)²

dy / dx + (2x / 1 + x²)y = 1 / (1 + x²)²

Comparing with dy / dx + Py = Q

IF = e^{∫P dx}

Let 1 + x² = t

2x dx = dt

dx = dt / 2

IF = e^{∫(2x / t) (dt / 2x)}

= e^{∫dt / t}

= e^{log |t|}

= t

IF = 1 + x²

Solution of the differential equation is y * IF = ∫Q * IF dx

y * (1 + x²) = ∫[1 / (1 + x²)²] * (1 + x²) dx

y * (1 + x²) = tan^-1 x + c

C = – 𝝿 / 4

y * (1 + x²) = tan^-1 x – 𝝿 / 4

Question 11[a]: The projection of the vector 2i + 3j + 2k on the vector i + j + k is

(a) 3 / √3 (b) 7 / √3 (c) 3 / √17 (d) 7 / √17

[b] Find the area of a parallelogram whose adjacent sides are the vectors 2i + j + k and i – j.

Solution:

|a x b| = i + j – 3k

|a x b| = √11

Question 12[a]: The angle between the vectors i + j and j + k is

(a) 60^o (b) 30^o (c) 45^o (d) 90^o

[b] If a, b, c are unit vectors such that a + b + c = 0, find the value of a . b + b . c + c . a.

Solution:

(a + b + c)² = 0

|a|² + |b|² + |c|² + 2ab + 2bc + 2ca = 0

3 + 2 (a . b + a . c + b . c) = 0

(a . b + a . c + b . c) = – 3 / 2

Question 13[a]: The line x – 1 = y = z is perpendicular to the line

(a) x – 2 / 1 = y – 1 / 2 = z / -3 (b) x – 2 = y – 2 = z

(c) x – 2 / 1 = y – 1 / 2 = z / -3 (d) x = y = 2 / 3

[b] Find the shortest distance between the lines r = i + 2j + 3k + ƛ (i + j + k) and r = i + j + k + 𝛍 (i + j + k).

Solution:

a₂ = i + j + k

b₁ = i + j + k

b₂ = i + j + k

a₂ – a₁ = – j – 2k

Shortest distance = |b x (a₂ – a₁) / |b|| = √2

Question 14[a]: Distance of the point (0, 0, 1) from the plane x + y + z = 3.

(a) 1 / √3 (b) 2 / √3 (c) √3 (d) √3 / 2

[b] Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to x – y + z = 0.

Solution:

(2ƛ + 1) x + (3ƛ + 1) y + (4ƛ + 1) z – 5ƛ – 1 = 0

(2ƛ + 1) (1) + (3ƛ + 1) (-1) + (4ƛ + 1) (1) = 0

ƛ = – 1 / 3

(x + y + z – 1) – (1 / 3) (2x + 3y + 4z – 5) = 0

x – z + 2 = 0

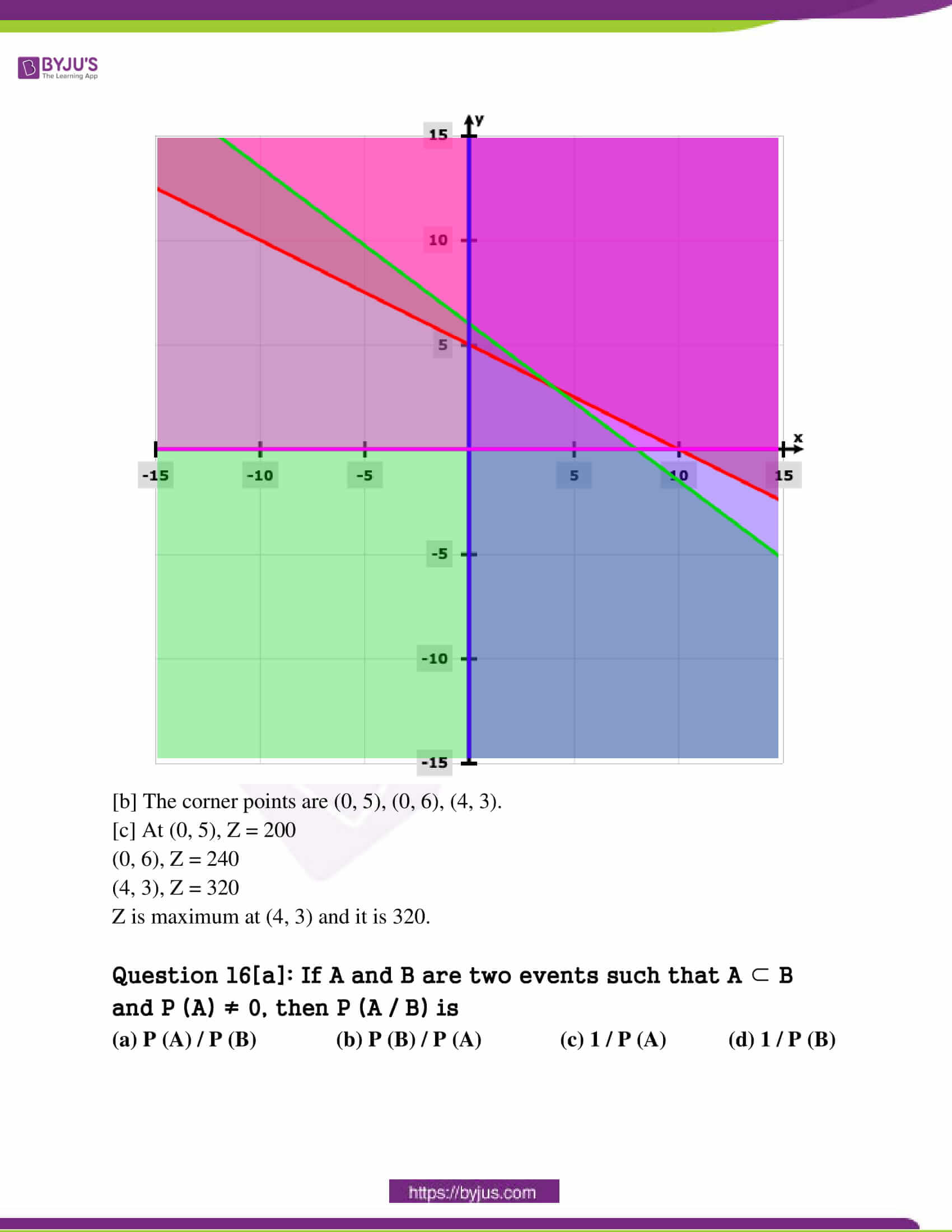
Question 15[a]: Consider the linear programming problem:

Maximise Z = 50x + 40y

Subject to constraints

x + 2y ≥ 10

3x + 4y ≤ 24

x ≥ 0, y ≥ 0

[a] Find the feasible region.

[b] Find the corner points of the feasible region.

[c] Find the maximum value of Z.

Solution:

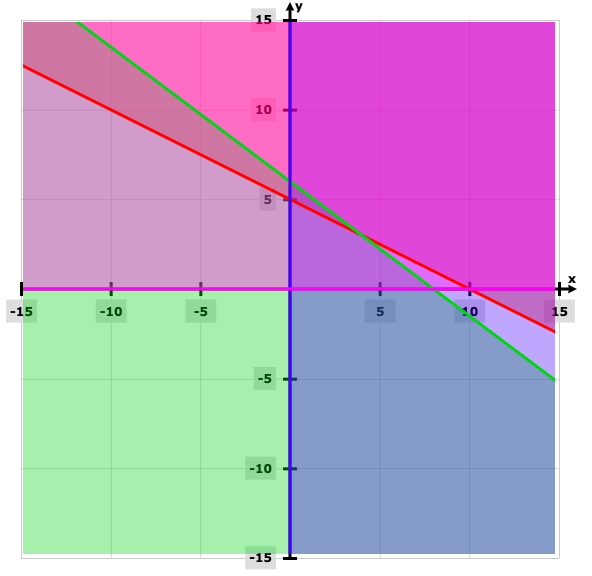
(0, 6), Z = 240

(4, 3), Z = 320

Z is maximum at (4, 3) and it is 320.

Question 16[a]: If A and B are two events such that A ⊂ B and P (A) ≠ 0, then P (A / B) is

(a) P (A) / P (B) (b) P (B) / P (A) (c) 1 / P (A) (d) 1 / P (B)

[b] There are two identical bags. The bag I contain 3 red and 4 black balls while Bag II contains 5 red and 4 black balls. One ball is drawn at random from one of the bags.

[i] Find the probability that the ball drawn is red.

[ii] If the ball drawn is red what is the probability that it was drawn from Bag I?

OR

Consider the following probability distribution of a random variable X.

[i] Find the value of K.

[ii] Determine the mean and variance of K.

Solution:

P (A / E1) = 5 / 9

P (A / E2) = 3 / 7

P (the ball drawn is red) = (1 / 2) (5 / 9) + (1 / 2) (3 / 7)

= 62 / 126

= 31 / 63

= (1 / 2) * (3 / 7) / (1 / 2) (5 / 9) + (1 / 2) (3 / 7)

= 27 / 62

OR

K = 7 / 16

= 0 + (2 / 16) + (14 / 16) + (15 / 16) + (4 / 16)

= 35 / 16

E (X²) = ∑X² * P (X)

= 0 + (2 / 16) + (28 / 16) + (45 / 16) + (16 / 16)

= 91 / 16

Variance = ∑X² * P (X) – [∑X * P (X)]²

= 91 / 16 – [35 / 16]²

= 231 / 256

= 0.902