Kerala Class 12th Maths Question Paper 2019 Solved – Free Download
Kerala Plus Two (Class 12) maths 2019 question paper with answers are provided here in a downloadable pdf format and also in the text, so that the students can use them to track their progress. Along with the solutions, Kerala Plus Two maths question paper 2019 Class 12 is also added here for effective preparation. Students are able to access all the Kerala board previous year maths question papers. The solution provided by BYJU’S will assist the students in improving their time management skills, as it is common that the students who are well prepared also face difficulty in finishing the question paper on time. It can be downloaded easily and in a shorter period of time. Solving 2019 Maths question papers and also the previous year papers for Class 12 plays a very important role in your preparation for the board exams.
Download Kerala Plus Two 2019 Maths Question Paper
Download Kerala Plus Two 2019 Maths Question Paper With Answers
KBPE Class 12th Maths Question Paper With Solution 2019
QUESTION PAPER CODE SY 27
Question 1 to 7 carries 3 scores each. Answer any six questions. [6 * 3 = 18]
Question 1[a]: If f (x) = sin x, g (x) = x2 ; x ∈ R; then find (fog) (x).
[b] Let u and v be two functions defined on R as u (x) = 2x – 3 and v (x) = (3 + x) / 2 . Prove that u and v are inverse to each other.
Solution:
[a] f (x) = sin xg (x) = x2
(fog) (x) = f (g (x))
= f (x2)
= sin (x2)
[b] (u o v) x = u (v (x)) = u ((3 + x) / 2))= [2 (3 + x) / 2] – 3 = x
(u o v) = I
(v o u) x = v (u (x))
= v (2x – 3)
= (3 + 2x – 3) / 2 = x
(v o u) = I
Question 2[a]: For the symmetric matrix A =  Find the values of x and y.
Find the values of x and y.
(b) From Part(a), verify AA’ and A + A’ are symmetric matrices.
Solution:
[a] x = 5 and y = 8 [b]

AA’ and A + A’ are symmetric matrices.
Question 3[a]: Find the slope of the tangent line to the curve y = x2 – 2x + 1.
(b) Find the equation of the tangent to the above curve which is parallel to the line 2x – y + 9 = 0.
Solution:
[a] y = x2 – 2x + 1dy / dx = 2x – 2
Slope of tangent line = 2x – 2
[b] Since the tangent is parallel to 2x – y + 9 = 0, the slopes are the same.2x – y + 9 = 0
y = 2x + 9
Slope = 2 [y = mx + c]
2x – 2 = 2
x = 2 and y = 1
The point is (2, 1).
The equation of the tangent is (y – y1) = (dy / dx) (x – x1)
(y – 1) = 2 (x – 2)
y – 2x + 3 = 0
Question 4[a]: If ∫f (x) dx = log |tan x| + C. Find f (x).
[b] Evaluate ∫1 / [√1 – 4x2] dx
Solution:
[a] ∫f (x) dx = log |tan x| + Cf (x) = sec2 x / tan x or 2 cosec 2x
[b] ∫1 / [√1 – 4x2] dx= ∫1 / [√4 (1 / 4 – x2)] dx
= (1 / 2) ∫1 / [√(1 / 2)2 – x2] dx
= (1 / 2) sin-1 (x / [1 / 2]) + C
= (1 / 2) sin-1 2x + C
Question 5[a]: Area bounded by the curve y = f (x) and the lines x = a, x = b and the x axis = ______
(i) ∫ab x dy (ii) ∫ab x2 dy (iii) ∫ab y dx (iv) ∫ab y2 dx
Answer: (iii)
[b] Find the area of the shaded region using integration.

Solution:
The curve is y = 3x.
Area = ∫12 y dx
= ∫12 3x dx
= 3 (x2 / 2)12
= 9 / 2
Question 6[a]: The order of the differential equation formed by y = A sin x + B cos x + c, where A and B are arbitrary constants is
(i) 1 (ii) 2 (iii) 0 (iv) 3
(b) Solve the differential equation sec2x tan y dx + sec2y tan x dy = 0.
Solution:
[a] (ii) or (iv) [b] sec2x tan y dx + sec2y tan x dy = 0 [sec2 x / tan x] dx + [sec2 y / tan y] dy = 0∫[sec2 x / tan x] dx + ∫[sec2 y / tan y] dy = 0
log |tan x| + log |tan y| = log C
tan x . tan y = C
Question 7: A factory produces three items P, Q and R at two plants A and B. The number of items produced and operating costs per hour is as follows :
|
Plant |
Item produced per hour |
Operating cost |
||
|
P |
Q |
R |
||
|
A |
20 |
15 |
25 |
Rs. 1000 |
|
B |
30 |
12 |
23 |
Rs. 800 |
It is desired to produce at least 500 items of type P, at least 400 items of type Q and at least 300 items of type R per day.
(a) Is it a maximization case or a minimization case. Why?
(b) Write the objective function and constraints.
Solution:
Minimum Z = 1000x + 800y
Subject to
20x + 30y ≥ 500
15x + 12y ≥ 400
25x + 23y ≥ 300
x, y ≥ 0
Questions 8 to 17 carry 4 scores each. Answer any eight. (8 * 4 = 32)
Question 8[a]: The function P is defined as “To each person on the earth is assigned a date of birth”. Is this function one-one ? Give reason.
(b) Consider the function f : [0, 𝛑 / 2] → R
given by f (x) = sin x and g : [0, 𝛑 / 2] → R
given by g (x) = cos x.
(i) Show that f and g are one-one functions.
(ii) Is f + g one-one? Why?
(c) The number of one-one functions from a set containing 2 elements to a set containing 3 elements is ______
(i) 2 (ii) 3 (iii) 6 (iv) 8
Solution:
[a] The function is not one-one because different persons can have the same birthday. [b] [i] f (x) = sin xf (x1) = f (x2)
sin x1 = sin x2
x1 = x2
Thus f is one to one.
g (x) = cos x
g (x1) = g (x2)
cos x1 = cos x2
x1 = x2
Thus g is one to one.
[ii] (f + g) (x) = sin x + cos x(f + g) (x1) = (f + g) (x2)
sin x1 + cos x1 = sin x2 + cos x2
sin x1 – sin x2 = cos x2 – cos x1
cos (x1 + x2) / 2 = sin (x1 + x2) / 2
x1 = (𝛑 / 2) – x2
f + g is not a one-one function.
[c] (iii)Question 9: If A = sin-1 (2x / [1 + x2]), B = cos-1 [1 – x2] / [1 + x2], C = tan-1 [2x / 1 – x2] satisfies the condition 3A – 4B + 2C = 𝛑 / 3. Find the value of x.
Solution:
A = sin-1 (2x / [1 + x2]) = sin-1 (sin 2θ) = 2θ
B = cos-1 [1 – x2] / [1 + x2] = cos-1 (cos 2θ) = 2θ
C = tan-1 [2x / 1 – x2] = tan-1 (tan θ) = 2θ
3A – 4B + 2C = 𝛑 / 3
3 (2θ) – 4 (2θ) + 2 (2θ) = 𝛑 / 3
6θ – 8θ + 4θ = 𝛑 / 3
2θ = 𝛑 / 3
tan-1 x = 𝛑 / 6
x = 1 / √3
Question 10[a]: Write the function whose graph is shown below.

(b) Discuss the continuity of the function obtained in part (a).
(c) Discuss the differentiability of the function obtained in part (a).
Solution:
[a] f (x) =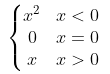 [b] lim x→0+ f (x) = lim x→0+ (x) = 0
[b] lim x→0+ f (x) = lim x→0+ (x) = 0
lim x→0- f (x) = lim x→0- (x2) = 0
f (0) = 0
f (x) is continuous at x = 0.
[c] f (x) is not differentiable at x = 0.Question 11: A cuboid with a square base and given volume ‘V’ is shown in the figure.

(a) Express the surface area ‘s’ as a function of x.
(b) Show that the surface area is minimum when it is a cube.
Solution:
[a] Surface area (S) = 2x2 + 4xyv = x2y
= 2x2 + 4x * (v / x2)
= 2x2 + (4v / x)
[b] ds / dx = 4x – (4v / x2)ds / dx = 0
v = x3
x = (v)⅓
d2s / dx2 = 4 + (8v / x3) = 4 + 8 = 12 > 0
Hence, S is minimum.
y = v / x2 = x3 / x2 = x
Therefore, cuboid becomes a cube.
Question 12[a]: If 2x + 4 = A (2x + 3) + B, find A and B.
[b] Using part (a) evaluate ∫{(2x + 4) / [x2 + 3x +1]}dx.
Solution:
[a] A = 1 and B = 1 [b] ∫{(2x + 4) / [x2 + 3x + 1]}dx= ∫{(2x + 3) / [x2 + 3x + 1]}dx + ∫{1 / [x2 + 3x + 1]}dx
= log |x2 + 3x + 1| + ∫{1 / [x2 + 3x + (9 / 4) – (9 / 4) + 1]}dx
= log |x2 + 3x + 1| + ∫1 / [(x + (3 / 2)2 – (√5 / 2)2]
= log |x2 + 3x + 1| + (1 / 2 * (√5 / 2)) log |(x + (3 / 2) – (√5 / 2)) / (x + (3 / 2) + (√5 / 2))
= log |x2 + 3x + 1| + [1 / √5] log |(x + [3 – √5] / 2) / (x + [3 + √5] / 2)|
Question 13: Consider the differential equation cos2x (dy / dx) + y = tan x. Find
(a) its degree
(b) the integrating factor
(c) the general solution.
Solution:
[a] one [b] IF = e∫P dx= e∫sec^2 x dx
= etan x
[c] y * etan x = ∫(tan x / cos2 x) * etan x dxPut u = tan x
y * etan x = ∫ueu du
= tan x etan x – etan x + C
Question 14: The position vectors of three points A, B, C are given to be i + 3 j + 3k, 4i + 4k and –2 i + 4 j + 2k, respectively.
(a) Find AB and AC.
(b) Find the angle between AB and AC.
(c) Find a vector which is perpendicular to both AB and AC having a magnitude 9 units.
Solution:
[a] AB = 3i – 3j + kBC = – 3i + j – k
[b] |AB| = √19|AC| = √11
cos θ = |[AB . AC] / [|AB| . |AC|]
= |(- 13) / [√19 . √11]|
= 13 / [√19 . √11]
θ = cos-1 [13 / [√19 . √11]] [c] n = (AB x AC) / |(AB x AC)|
= 2i – 6k
|AB x AC| = √40
The required vector = 9 (2i – 6k) / √40
Question 15[a]: If a, b, c are coplanar vectors, write the vector perpendicular to a.
(b) If a, b, c are coplanar, prove that a + b, b + c, c + a are coplanar.
Solution:
[a] (a x b) or (b x c) or (a x c) or (b x a) or (c x b) or (c x a) [b] [a b c] = 0 [a + b, b + c, c + a] = (a + b) . [(b + c) x (c + a)]= (a + b) . [(b x c) + (b x a) + (c x c) + (c x a)]
= a . (b x c) + b . (c x a)
= 2 [a b c]
= 0
So, a + b, b + c, c + a are coplanar.
Question 16[a]: Write all the direction cosines of the x-axis.
(b) If a line makes angles ɑ, β, 𝝲 with x, y, z axes respectively, then prove that sin2 ɑ + sin2 β + sin2 𝝲 = 2.
(c) If a line makes equal angles with the three coordinate axes, find the direction cosines of the lines.
Solution:
[a] 1, 0, 0 or cos 0, cos 90, cos 90 [b] cos2 ɑ + cos2 β + cos2 𝝲 = 1(1 – sin2 ɑ) + (1 – sin2 β) + (1 – sin2 𝝲) = 1
sin2 ɑ + sin2 β + sin2 𝝲 = 2
[c] ɑ = β = 𝝲cos ɑ = cos β = cos 𝝲
cos2 ɑ + cos2 β + cos2 𝝲 = 1
3 cos2 ɑ = 1
cos ɑ = 1 / √3
Similarly, β = 1 / √3 and 𝝲 = 1 / √3
Question 17: The activities of a factory are given in the following table:
|
Items |
Departments |
Profit per unit |
||
|
Cutting |
Mixing |
Packing |
||
|
A |
1 |
3 |
1 |
Rs. 5 |
|
B |
4 |
1 |
1 |
Rs. 8 |
|
Maximum time available |
24 |
21 |
9 |
Solve the linear programming problem graphically and find the maximum profit subject to the above constraints.
Solution:
x + 4y ≤ 24
3x + y ≤ 21
x + y ≤ 9
x, y ≥ 0
Maximise Z = 5x + 8y

(0, 0) = 0
(7, 0) = 35
(6, 3) = 54
(4, 5) = 60
(0, 6) = 48
Z is maximum at (4, 5) = 60.
Questions from 18 to 24 carry 6 scores each. Answer any five. (5 * 6 = 30)
Question 18: If A =  Show that A2 – 5A + 7I = 0. Hence find A4 and A-1.
Show that A2 – 5A + 7I = 0. Hence find A4 and A-1.
Solution:

Multiply by A-1
A-1 (A2 – 5A + 7I) = 0
A – 5I + 7A-1 = 0
7A-1 = 5I – A
A-1 =

Question 19: If A =  then
then
[a] Find A-1
[b] Use A–1 from part (a) solve the system of equations
2x – 3y + 5z = 11
3x + 2y – 4z = –5
x + y – 2z = –3
Solution:

The inverse matrix is on the right.
[b]

Question 20: Find dy / dx for the following.
[a] sin2x + cos2y = 1
(b) y = xx
(c) x = a (t – sin t); y = a (1 + cos t)
Solution:
[a] sin2x + cos2y = 12 sin x cos x + 2 cos y (- sin y) (dy / dx) = 0
cos y (- sin y) (dy / dx) = – sin x cos x
dy / dx = sin x cos x / sin y cosy
[b] y = xxlog y = x log x
(1 / y) (dy / dx) = x * (1 / x) + log x
dy / dx = y [1 + log x]
= xx [1 + log x] [c] x = a (t – sin t); y = a (1 + cos t)
dx / dt = a (1 – cos t)
dy / dt = – a sint
dy / dx = (dy / dt) / (dx / dt)
= – a sint / a (1 – cos t)
= – sint / 1 – cost
= – cot (t / 2)
Question 21: Evaluate the following integrals.
[a] ∫0𝛑/2 [(sin x) / [sin x + cos x]] dx
[b] ∫-𝛑/2𝛑/2 sin7 x dx
[c] ∫x sin 3x dx
Solution:
[a] ∫0𝛑/2 [(sin x) / [sin x + cos x]] dxI = ∫0𝛑/2 [(sin x) / [sin x + cos x]] dx
= ∫0𝛑/2 [sin (𝛑 / 2 – x)] / [sin (𝛑 / 2 – x + cos (𝛑 / 2 – x)]
= ∫0𝛑/2 [cos x / cos x + sin x] dx
2I = ∫0𝛑/2 1 dx
= [x]0𝛑/2
= 𝛑 / 2
I = 𝛑 / 4
[b] ∫-𝛑/2𝛑/2 sin7 x dx = 0Since it is an odd function.
[c] ∫x sin 3x dx= x ∫sin 3x dx – ∫1 [∫sin 3x dx] dx
= x . [- cos 3x / 3] – ∫[- cos 3x / 3]dx
= [- x cos 3x / 3] + sin 3x / 9 + C
Question 22: (a) Find the area bounded by the curve y = sin x and the lines x = 0, x = 2𝛑, and x-axis.
(b) Two fences are made in a grass field as shown in the figure. A cow is tied at the point O with a rope of length 3 m.

(i) Using integration, find the maximum area of grass that cows can graze within the fences. Choose O as the origin.
(ii) If there are no fences, find the maximum area of grass that cow can graze?
Solution:
[a] Area = ∫ab y dx= 4 ∫0𝛑/2 sin x dx
= 4 * 1
= 4
[b] [i]

The equation of the curve is x2 + y2 = 9.
y = √9 – x2
Area = ∫ab y dx
= ∫03 √9 – x2 dx
= [(x / 2) √9 – x2 + (9 / 2) sin-1 (x / 3)]03
= (9 / 2) sin-1 (1)
= 9𝛑 / 4 square units
[ii] Required area = 4 * (9𝛑 / 4)= 9𝛑 square units
Question 23: [a] Find the equation of the plane through the intersection of the planes 3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).
(b) The Cartesian equation of two lines are given by x + 1 / 7 = y + 1 / –6 = z + 1 / 1 and x – 3 / 1 = y – 5 / –2 = z – 7 / 1 . Write the vector equation of these two lines.
(c) Find the shortest distance between the lines mentioned in part (b).
Solution:
[a] (3x – y + 2z – 4) + k (x + y + z – 2) = 0It passes through (2, 2, 1).
[3 * 2 – 2 + 2 * 1 – 4] + k [2 + 2 + 1 – 2] = 0k = – 2 / 3
(3x – y + 2z – 4) – (2 / 3) (x + y + z – 2) = 0
7x – 5y + 4z – 8 = 0
[b] r = (- i – j – k) + ƛ (7i – 6j + k)r = (3i + 5j + 7k) + 𝛍 (i – 2j + k)
[c] Shortest distance = |(a2 – a1) . (b1 x b2) / |(b1 x b2)||(a2 – a1) = 4i + 6j + 8k
(b1 x b2) = – 4i – 6j – 8k
SD = |- 116 / √116| = √116
Question 24: [a] A bag contains 4 red and 4 black balls. Another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag and which is found to be red. Find the probability that the ball is drawn from the first bag.
(b) A random variable X has the following distribution function :
|
X |
0 |
1 |
2 |
3 |
4 |
|
P (x) |
k |
3k |
5k |
7k |
4k |
(i) Find k.
(ii) Find the mean and the variance of the random variable x.
Solution:
[a] Let E1 be the event of choosing bag I and E2 be the event of choosing bag II, also A be the event of choosing a red ball.P (E1) = P (E2) = 0.5
P (A / E1) = 4 / 8 = 1 / 2
P (A / E2) = 2 / 8 = 1 / 4
P (E1 / A) = [P (E1) * P (A / E1)] / [P (E1) * P (A / E1) + P (E2) * P (A / E2)]
= (0.5 * 0.5) / [(0.5 * 0.5) + (0.5 * 0.25)
= 2 / 3
[b] [i] ∑Pi = 1k + 3k + 5k + 7k + 4k = 1
20k = 1
k = 1 / 20
[ii]|
X |
0 |
1 |
2 |
3 |
4 |
|
P (x) |
1 / 20 |
3 / 20 |
5 / 20 |
7 / 20 |
4 / 20 |
|
X * P(x) |
0 |
3 / 20 |
10 / 20 |
21 / 20 |
16 / 20 |
|
X2 * P(x) |
0 |
3 / 20 |
20 / 20 |
63 / 20 |
64 / 20 |
Mean = ∑ x * P(x) = 50 / 20 = 5 / 2
Variance = ∑ x2 * P(x) – [∑ x * P(x)]2 = 5 / 4




















Comments