An exponential function is a mathematical function, which is used in many real-world situations. It is mainly used to find the exponential decay or exponential growth or to compute investments, model populations and so on. In this article, you will learn about exponential function formulas, rules, properties, graphs, derivatives, exponential series and examples.
Table of Contents:
- Definition
- Formula
- Graph
- Derivative
- Series
- Properties
- Rules
- Examples
- Solved Problems
- Practice Questions
What is Exponential Function?
An exponential function is a Mathematical function in the form f (x) = ax, where “x” is a variable and “a” is a constant which is called the base of the function and it should be greater than 0. The most commonly used exponential function base is the transcendental number e, which is approximately equal to 2.71828.
Exponential Function Formula
An exponential function is defined by the formula f(x) = ax, where the input variable x occurs as an exponent. The exponential curve depends on the exponential function and it depends on the value of the x.
The exponential function is an important mathematical function which is of the form
f(x) = ax
Where a>0 and a is not equal to 1.
x is any real number.
If the variable is negative, the function is undefined for -1 < x < 1.
Here,
“x” is a variable
“a” is a constant, which is the base of the function.
An exponential curve grows, or decay depends on the exponential function. Any quantity that grows or decays by a fixed per cent at regular intervals should possess either exponential growth or exponential decay.
Exponential Growth
In Exponential Growth, the quantity increases very slowly at first, and then rapidly. The rate of change increases over time. The rate of growth becomes faster as time passes. The rapid growth is meant to be an “exponential increase”. The formula to define the exponential growth is:
y = a ( 1+ r )x
Where r is the growth percentage.
Exponential Decay
In Exponential Decay, the quantity decreases very rapidly at first, and then slowly. The rate of change decreases over time. The rate of change becomes slower as time passes. The rapid growth meant to be an “exponential decrease”. The formula to define the exponential growth is:
y = a ( 1- r )x
Where r is the decay percentage.
Exponential Function Graph
The following figure represents the graph of exponents of x. It can be seen that as the exponent increases, the curves get steeper and the rate of growth increases respectively. Thus, for x > 1, the value of y = fn(x) increases for increasing values of (n).

From the above, it can be seen that the nature of polynomial functions is dependent on their degree. The higher the degree of any polynomial function, the higher its growth. A function which grows faster than a polynomial function is y = f(x) = ax, where a>1. Thus, for any of the positive integers n the function f (x) is said to grow faster than that of fn(x).
Thus, the exponential function having base greater than 1, i.e., a > 1 is defined as y = f(x) = ax. The domain of exponential function will be the set of entire real numbers R and the range are said to be the set of all the positive real numbers.
It must be noted that the exponential function is increasing and the point (0, 1) always lies on the graph of an exponential function. Also, it is very close to zero if the value of x is mostly negative.
Exponential function having base 10 is known as a common exponential function. Consider the following series:

The value of this series lies between 2 & 3. It is represented by e. Keeping e as the base of the function, we get y = ex, which is a very important function in mathematics known as a natural exponential function.
For a > 1, the logarithm of b to base a is x if ax = b. Thus, loga b = x if ax = b. This function is known as logarithmic function.

For base a = 10, this function is known as a common logarithm and for the base a = e, it is known as a natural logarithm denoted by ln x. Following are some of the important observations regarding logarithmic functions which have a base a>1.
- The domain of log function consists of positive real numbers only, as we cannot interpret the meaning of log functions for negative values.
- For the log function, though the domain is only the set of positive real numbers, the range is a set of all real values, i.e. R
- When we plot the graph of log functions and move from left to right, the functions show increasing behaviour.
- The graph of log function never cuts the x-axis or y-axis, though it seems to tend toward them.

- Logap = α, logbp = β and logba = µ, then aα = p, bβ = p and bµ = a
- Logbpq = Logbp + Logbq
- Logbpy = ylogbp
- Logb (p/q) = logbp – logbq
Exponential Function Derivative
Let us now focus on the derivative of exponential functions.
The derivative of ex with respect to x is ex, i.e. d(ex)/dx = ex
It is noted that the exponential function f(x) =ex has a special property. It means that the derivative of the function is the function itself.
Exponential Series
The exponential series are given below.
Exponential Function Properties
The exponential graph of a function represents the exponential function properties.
Let us consider the exponential function, y = 2x
The graph of function y = 2x is shown below.
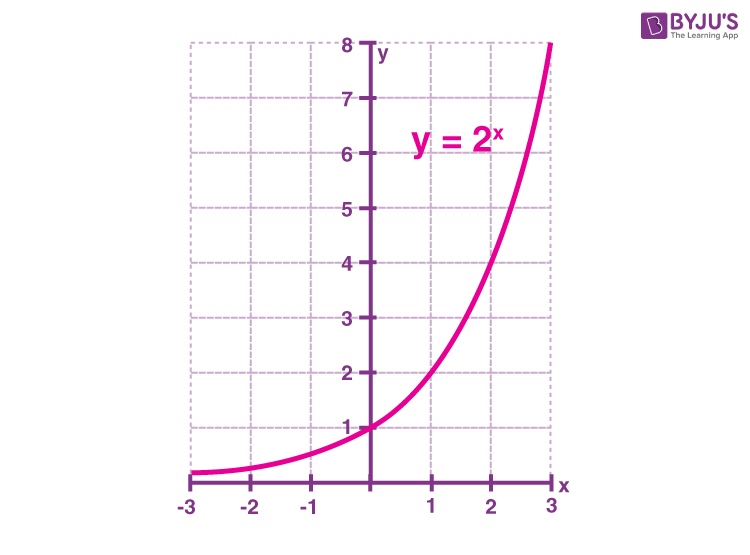
Exponential Function Graph for y = 2x
The properties of the exponential function graph when the base is greater than 1 are given below.
- The graph passes through the point (0,1).
- The domain is all real numbers
- The range is y>0
- The graph is increasing
- The graph is asymptotic to the x-axis as x approaches negative infinity
- The graph increases without bound as x approaches positive infinity
- The graph is continuous
- The graph is smooth

Exponential Function Graph y=2-x
The graph of function y=2-x is shown above. The properties of the exponential function and its graph when the base is between 0 and 1 are given.
- The line passes through the point (0,1)
- The domain includes all real numbers
- The range is of y>0
- It forms a decreasing graph
- The line in the graph above is asymptotic to the x-axis as x approaches positive infinity
- The line increases without bound as x approaches negative infinity
- It is a continuous graph
- It forms a smooth graph
Exponential Function Rules
Some important exponential rules are given below:
If a>0, and b>0, the following hold true for all the real numbers x and y:
-
- ax ay = ax+y
- ax/ay = ax-y
- (ax)y = axy
- axbx=(ab)x
- (a/b)x= ax/bx
- a0=1
- a-x= 1/ ax
Exponential Functions Examples
The examples of exponential functions are:
- f(x) = 2x
- f(x) = 1/ 2x = 2-x
- f(x) = 2x+3
- f(x) = 0.5x
Solved Problems
Question 1:
Simplify the exponential function 2x – 2x+1
Solution:
Given exponential function: 2x – 2x+1
By using the property: ax ay = ax+y
Hence, 2x+1 can be written as 2x. 2
Thus the given function is written as:
2x-2x+1 = 2x-2x. 2
Now, factor out the term 2x
2x-2x+1 = 2x-2x. 2 = 2x(1-2)
2x-2x+1 = 2x(-1)
2x-2x+1 = – 2x
Therefore, the simplification of the given exponential function 2x – 2x+1 is – 2x.
Question 2:
Solve the exponential equation: (¼)x = 64
Solution:
Given exponential equation is:
(¼)x = 64
Using the exponential rule (a/b)x = ax/bx, we get;
1x/4x = 43
1/4x = 43 [since 1x = 1]
(1)(4-x) = 43
4-x = 43
Here, bases are equal.
So, by equating the powersm we have;
Practice Questions
- Graph an exponential function (⅓)x – 1.
- Solve for x: 8(4x-1) = 45x
- Solve the exponential equation for x: -5x-3 = 25/40

Comments