The inverse sine function (also called arcsine) is the inverse of sine function. Since sine of an angle (sine function) is equal to ratio of opposite side and hypotenuse, thus sine inverse of same ratio will give the measure of the angle. Let’s say θ is the angle, then:
sin θ = (Opposite side to θ/Hypotenuse)
Or θ = Sin-1 (Opposite side to θ/Hypotenuse)
In the same way, Inverse Cosine and Inverse Tan can be determined.
| Fact: If the ratio of opposite side of angle θ and hypotenuse equals to 1, then,
θ = sin-1 (1) = sin-1 (sin 90) = 90 degrees |
The function of inverse or inverse function is used to determine the angle measure, with the use of basic trigonometric ratios from the right triangle. Mostly, the inverse sine function is represented using sin-1. It does not mean that sine is not raised to the negative power.
| Table of contents: |
What is Sine Function?
In a right-angle triangle, a sine function of an angle θ is equal to the opposite side to θ divided by hypotenuse.
Sin θ = Opposite side/Hypotenuse
This is the basic formula for sine function. See the figure below.
Sin θ = Opposite / Hypotenuse
What is Inverse Sine Function?
In the above explanation, we learned about sine function, where we can determine the sin of any angle if the opposite side and hypotenuse is known to us.
What if we have to find just the measure of angle θ? The inverse sine function or Sin-1 takes the ratio, Opposite Side / Hypotenuse Side and produces angle θ. It is also written as arcsin.
Sin inverse is denoted by sin-1 or arcsin
θ = Sin-1 (Opposite side/Hypotenuse)
Let us see an example of inverse of sine function.
Example: In a triangle, ABC, AB= 4.9m, BC=4.0 m, CA=2.8 m and angle B = 35°.
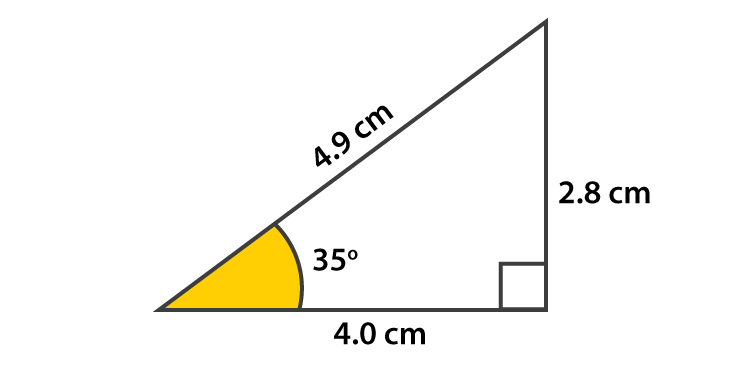
Solution:
- Sin 35° = Opposite / Hypotenuse
- Sin 35° = 2.8 / 4.9
- Sin 35° = 0.57°
So, Sin-1 (Opposite / Hypotenuse) = 35°
Sin-1 (0.57) = 35°
Also, read:
Inverse Sine Formula
Let us consider if we want to find the depth(d) of the seabed from the bottom of the ship and the following two parameters are given:
- The angle which the cable makes with the seabed.
- The cable’s length.
The Sine function will help to find the distance/depth d of the ship from the sea bed by the following method:
If the angle is 39° and the cable’s length is 40 m.
- Sin 39° = Opposite / Hypotenuse
- Sin 39° = d / 40
- d = Sin 39° × 40
- d = 0.6293 × 40
- d = 25.172 cm
Therefore, the depth d is 25.17 cm.
Summary of Formula:
The formula for the trigonometric sine function is given by:
sin (θ) Opposite Side/ Hypotenuse
The inverse sine function formula or the arcsin formula is given as:
sin-1 (Opposite side/ hypotenuse) = θ
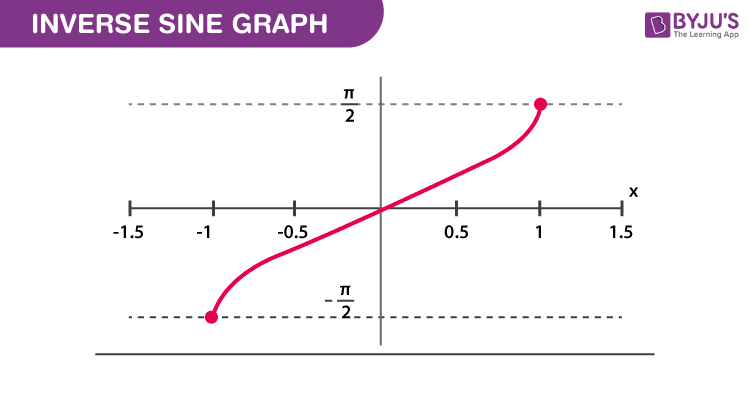
Graph of Inverse Sine Function
Arcsine trigonometric function is the sine function is shown as sin-1 a and is shown by the below graph.
Inverse Sine Derivative
The derivative of inverse sine function is given by: d/dx Sin-1x= 1 / √(1-x2)
Let us proof this equation.
Proof: f(x) =sin(x) and g(x) = sin-1x
If we differentiate g(x) with respect to x, we get;
g'(x) = 1/f'(g(x)) = 1/cos(sin-1x) …………….(1)
Now we know, the inverse of sine function, y = Sin-1x
or sin y = x …………(2)
Hence we can write, the derivative as;
g'(x) = 1/cos y (from eq.1)
Since, we know, by trigonometric identities;
cos2 y + sin2 y = 1
Therefore, we can write;
cos y = √(1-sin2 y) = √(1 – x2) (since sin y = x)
Now, again putting this value in the derivative;
g'(x) = 1/cos y = 1/√(1 – x2)
Thus,
d/dx(sin-1x) = 1/√(1 – x2)
Inverse Sine Table
| θ | Sin-1 or Arcsin(θ) (in Radian) | Sin-1 or Arcsin(θ) (in Degree) |
| -1 | -π/2 | -90° |
| -√3/2 | -π/3 | -60° |
| -√2/2 | -π/4 | -45° |
| -1/2 | -π/6 | -30° |
| 0 | 0 | 0° |
| 1/2 | π/6 | 30° |
| √2/2 | π/4 | 45° |
| √3/2 | π/3 | 60° |
| 1 | π/2 | 90° |
Solved Examples
Now, if the angle is not given and we want to calculate it, then we use the Inverse functions and the question will be asked in the following way:
Problem: What is the angle Sin = Opposite / Hypotenuse, has?
Solution: Let’s take the measurement from above example only.
- Distance d = 25.17 cm
- Cable’s length = 40 cm.
We want to find the angle “α ”
Step 1: Find the sin α°
- Sin α° = Opposite / Hypotenuse
- Sin α° = 25.17 / 40
- Sin α° = 0.6293
Step 2: Now, for which angle sin α° = 0.6293
Let’s find it out with Inverse sin:
α° = Sin-1 / (0.6293)
α° = 38.1°
Did you know: Sin and Sin-1 are vice-versa.
Example: Sin 30° = 0.5 and Sin-1 (0.5) = 30°
| Did you know: Sin and Sin-1 are vice-versa.
Example: Sin 30° = 0.5 and Sin-1 (0.5) = 30° |
Need to practice more on the trigonometric functions, Download BYJUS -The learning app.
Frequently Asked Questions – FAQs
What is inverse sine?
α = sin-1 (opposite side of α/hypotenuse)
Where sin-1 represents the sine inverse function.
What is the value of sin inverse of 1?
α = sin-1(1)
We know that, sin 90 degrees = 1
Therefore, α = sin-1 (sin 90) = 90 degrees



Comments