Rajasthan Board Class 9 Maths Syllabus 2021-22

Rajasthan State Board Class 9 syllabus is prescribed by the Board of Secondary Education, Rajasthan, in short RSEB. The board mainly focuses on the promotion and development of secondary education in the state of Rajasthan. The Rajasthan Board Class 9 Maths Syllabus is designed by a group of subject experts who are well trained and experienced in mathematics.

The syllabus is the backbone of every subject. It provides a framework to the students and teachers for the sequential understanding of a subject. Especially when subjects are like Mathematics, referring syllabus is almost unavoidable if he/she is expecting to score high. Rajasthan Board Class 9 Mathematics Syllabus under RSEB incorporates a wide spectrum of topics starting from algebra to geometry. To master mathematics, he/she has to finish practising entire Rajasthan Board Class 9 Textbook. The only most coherent way to achieve this is following syllabus.

RBSE Class 9 Maths Syllabus 2021-22

Class 9 mathematics syllabus is divided into a total of 6 units and comprises chapters like Number system, polynomials, equations in two variables, Euclid’s geometry and probability, etc. Have a look at the table below to know the detailed class 9 Mathematics Syllabus of Rajasthan Board. Moreover, students can also download the pdf from the link given.

Download Rajasthan Board Class 9 Maths 2021-22 Syllabus PDF

RBSE Class 9 Maths 2021-22 Syllabus Unit Wise Marks Weightage

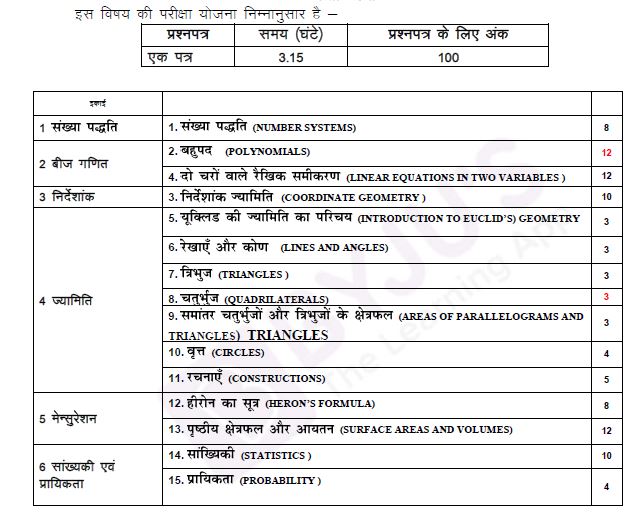
Details of the syllabus are as follows:

1. NUMBER SYSTEMS
   Irrational Numbers , Real Numbers and their Decimal Expansions ,Representing Real Numbers on the Number Line, Operations on Real Numbers, Laws of Exponents for Real Numbers.
2. POLYNOMIALS
   Polynomials in One Variable, Zeroes of a Polynomial ,Remainder Theorem , Factorisation of Polynomials Algebraic Identities.
3. COORDINATE GEOMETRY
   Cartesian System ,Plotting a Point in the Plane if its Coordinates are given.
4. LINEAR EQUATIONS IN TWO VARIABLES,  Linear Equations ,Solution of a Linear Equation ,Graph of a Linear Equation in Two Variables ,Equations of Lines Parallel to x-axis and y-axis.
5. INTRODUCTION TO EUCLID’S GEOMETRY
   Euclid’s Definitions, Axioms and Postulates,Equivalent Versions of Euclid’s Fifth Postulate.
6. LINES AND ANGLES
   Basic Terms and Definitions, Intersecting Lines and Non-intersecting Lines,Pairs of Angles,
   Parallel Lines and a Transversal,Lines Parallel to the same Line,Angle Sum Property of a
   Triangle.
7. TRIANGLES
   Congruence of Triangles ,Criteria for Congruence of Triangles,Some Properties of a Triangle,
   Some More Criteria for Congruence of Triangles ,Inequalities in a Triangle.
8. QUADRILATERALS
   Angle Sum Property of a Quadrilateral ,Types of Quadrilaterals ,Properties of a Parallelogram ,
   Another Condition for a Quadrilateral to be a Parallelogram ,The Mid-point Theorem.
9. AREAS OF PARALLELOGRAMS AND TRIANGLES
   Figures on the same Base and Between the same Parallels ,Parallelograms on the same Base
   and,between the same Parallels, Triangles on the same Base and between,the same Parallels.
10. CIRCLES
    Circles and its Related Terms: A Review,Angle Subtended by a Chord at a Point,Perpendicular
    from the Centre to a Chord,Circle through Three Points,Equal Chords and their Distances from
    the Centre ,Angle Subtended by an Arc of a Circle,Cyclic Quadrilaterals.
11. CONSTRUCTIONS
    Basic Constructions, Some Constructions of Triangles.
12. HERON’S FORMULA
    Area of a Triangle – by Heron’s Formula. Application of Heron’s Formula in finding, Areas of
    Quadrilaterals.
13. SURFACE AREAS AND VOLUMES
    Surface Area of a Cuboid and a Cube, Surface Area of a Right Circular Cylinder ,Surface Area
    of a Right Circular Cone ,Surface Area of a Sphere,Volume of a Cuboid, Volume of a Cylinder,
    Volume of a Right Circular Cone, Volume of a Sphere.
14. STATISTICS
    Collection of Data,Presentation of Data,Graphical Representation of Data, Measures of
    Central Tendency.
15. PROBABILITY
    Probability – an Experimental Approach

Keep Learning and stay tuned for the latest updates on Rajasthan Board Exam. Moreover, students can access interactive lessons and videos of Maths and Science through BYJU’S Tablet/App.