RBSE Class 12 Maths Chapter 3 – Matrix Important questions and solutions are provided here. All the important questions and solutions of matrices of Class 12 available here contain stepwise solutions. The RBSE Class 12 important questions and solutions available at BYJU’S will guide the students in clearing the exams with flying colours.
Chapter 3 of RBSE Class 12 has two exercises which cover various concepts of matrices along with the required solved examples. This chapter contains questions in different patterns such as finding the order of a given matrix, finding the given matrix when a particular equation is provided to get the elements of that matrix. Also, students will learn simple arithmetic operations on matrices, namely addition, subtraction and multiplication.
RBSE Maths Chapter 3: Exercise 3.1 Textbook Important Questions and Solutions
Question 1: If \(\begin{array}{l}\begin{bmatrix} k+4 & -1\\ 3 & k-6 \end{bmatrix} = \begin{bmatrix} a & -1\\ 3 & -4 \end{bmatrix}\end{array} \)
, then find the value of a.
Solution:
Given,
\(\begin{array}{l}\begin{bmatrix} k+4 & -1\\ 3 & k-6 \end{bmatrix} = \begin{bmatrix} a & -1\\ 3 & -4 \end{bmatrix}\end{array} \)
By equating the corresponding elements,
k – 6 = -4
k = 6 – 4
k = 2
And
k + 4 = a
2 + 4 = a
⇒ a = 6
Question 2: Find a matrix A = [aij] of order 2 x 2 whose elements are defined by aij = 2i – 3j.
Solution:
Given,
aij = 2i – 3j
a11 = 2(1) – 3(1) = 2 – 3 = -1
a12 = 2(1) – 3(2) = 2 – 6 = -4
a21 = 2(2) – 3(1) = 4 – 3 = 1
a22 = 2(2) – 3(2) = 4 – 6 = -2
Therefore, the required matrix
\(\begin{array}{l}=\begin{bmatrix} -1 & -4\\ 1 & -2 \end{bmatrix}\end{array} \)
Question 3: Find the values of a and b, if
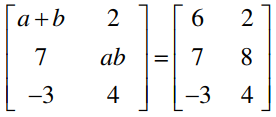
Solution:
Given,
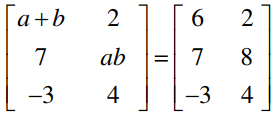
By comparing the corresponding elements,
a + b = 6
b = 6 – a ….(i)
ab = 8 ….(ii)
From (i) and (ii),
a(6 – a)= 8
6a – a2 – 8=0
⇒ a2 – 6a + 8 = 0
⇒ a2 – 2a – 4a + 8 = 0
⇒ a(a – 2) – 4(a – 2) = 0
⇒ (a – 2)(a – 4) = 0
⇒ a – 2 = 0, a – 4 = 0
⇒ a = 2, a = 4
If a = 2, b = 6 – 2 = 4
If a = 4, b = 6 – 4 = 2
Therefore, the values of a and b are 2, 4 and 4, 2, respectively.
Question 4: For what values of a, b and c, matrices A and B are equal matrices. Where:
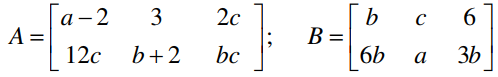
Solution:
Given,
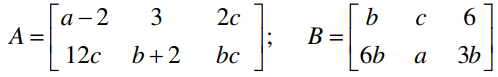
By equating the corresponding terms,
a – 2 = b
⇒ a – b = 2 …(i)
3 = c
12c = 6b
⇒ b = 12c/6 = 2c = 2 × 3 = 6
From (i),
a – 6 = 2
a = 2 + 6 = 8
Therefore, a = 8, b = 6 and c = 3.
RBSE Maths Chapter 3: Exercise 3.2 Textbook Important Questions and Solutions
Question 5: If \(\begin{array}{l}A=\begin{bmatrix} -3& 2& 1\\ 1 & -4 & 7 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B=\begin{bmatrix} 3& 5& -2\\ -1 & 4 & -2 \end{bmatrix}\end{array} \)
, then find A + B and A – B.
Solution:
Given,
\(\begin{array}{l}A=\begin{bmatrix} -3& 2& 1\\ 1 & -4 & 7 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B=\begin{bmatrix} 3& 5& -2\\ -1 & 4 & -2 \end{bmatrix}\end{array} \)
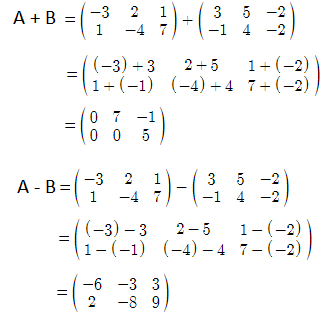
Question 6: If \(\begin{array}{l}A = \begin{bmatrix} 1 & 3\\ 2 & 1\\ 3 & -1 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B = \begin{bmatrix} 2 & 1\\ 1 & 2\\ -1 & 0 \end{bmatrix}\end{array} \)
, then find matrix C where A + 2B + C = O and O is a zero matrix.
Solution:
Given,
\(\begin{array}{l}A = \begin{bmatrix} 1 & 3\\ 2 & 1\\ 3 & -1 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B = \begin{bmatrix} 2 & 1\\ 1 & 2\\ -1 & 0 \end{bmatrix}\end{array} \)
Now,
A + 2B + C = O
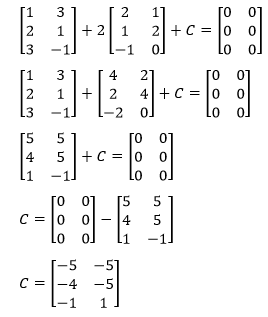
Question 7: If \(\begin{array}{l}A=\begin{bmatrix} 0 & 1 & 2 & 3\\ 3 & 2 & 1 & 0 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B = \begin{bmatrix} 0 & 3\\ 1& 2\\ 2 & 1\\ 3& 0 \end{bmatrix}\end{array} \)
, then show that AB ≠ BA.
Solution:
Given,

Therefore, AB ≠ BA
Question 8: Prove that:
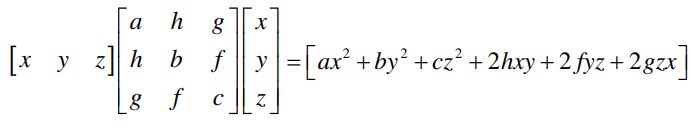
Solution:
LHS =
\(\begin{array}{l}\begin{bmatrix} x & y & z \end{bmatrix}\begin{bmatrix} a & h & g\\ h & b & f\\ g & f & c \end{bmatrix}\begin{bmatrix} x\\ y\\ z\end{bmatrix}\end{array} \)
\(\begin{array}{l}=\begin{bmatrix} ax+hy+gz & hx+by+fz & gx+fy+cz \end{bmatrix}\begin{bmatrix} x\\ y\\ z\end{bmatrix}\end{array} \)
= (ax + hy + gz)x + (hx + by + fz)v + (gr + fy + cz)z
= ax2 + hxy + gzx + hxy + by2 + fyz + gzx + fyz + cz2
= ax2 + by2 + cz2 + 2hxy + 2fyz + 2gzx
= RHS
Hence Proved.
Question 9: If \(\begin{array}{l}A=\begin{bmatrix} 1 & 0\\ -1 &7 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}I=\begin{bmatrix} 1 & 0\\ 0 &1 \end{bmatrix}\end{array} \)
, then find the value of K where A2 = 8A + KI.
Solution:
Given,
\(\begin{array}{l}A=\begin{bmatrix} 1 & 0\\ -1 &7 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}I=\begin{bmatrix} 1 & 0\\ 0 &1 \end{bmatrix}\end{array} \)
Consider, A2 = 8A + KI
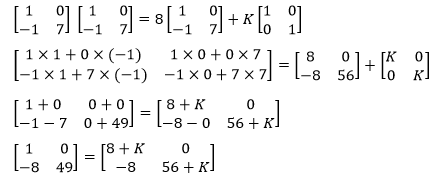
Now, by equating the corresponding elements,
1 = 8 + K
⇒ K = 1 – 8 = -7
Therefore, the value of K = -7.
Question 10: If \(\begin{array}{l}A=\begin{pmatrix} cos\alpha &sin\alpha \\ -sin\alpha &cos\alpha \end{pmatrix}\end{array} \)
, then prove that \(\begin{array}{l}A^n=\begin{pmatrix} cos\ n\alpha &sin\ n\alpha \\ -sin\ n\alpha &cos\ n\alpha \end{pmatrix}\end{array} \)
, where n is a positive integer.
Solution:
Given,
\(\begin{array}{l}A=\begin{pmatrix} cos\alpha &sin\alpha \\ -sin\alpha &cos\alpha \end{pmatrix}\end{array} \)
A2 = A.A
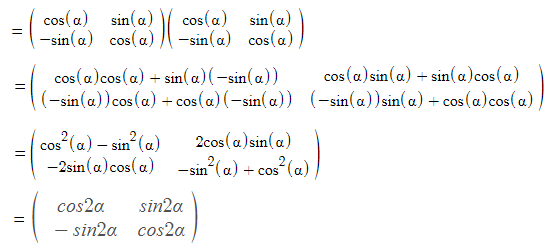
A3 = A2.A
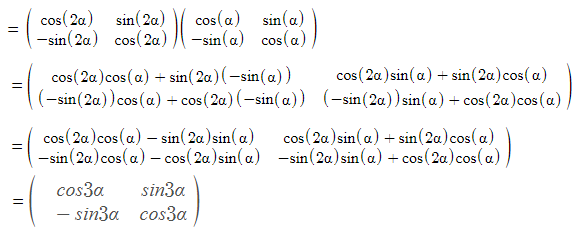
Similarly,
\(\begin{array}{l}A^n=\begin{pmatrix} cos\ n\alpha &sin\ n\alpha \\ -sin\ n\alpha &cos\ n\alpha \end{pmatrix}\end{array} \)
Hence proved.
RBSE Maths Chapter 3: Additional Important Questions and Solutions
Question 1: If \(\begin{array}{l}A=\begin{bmatrix} -i & 0\\ 0& i \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B=\begin{bmatrix} 0& i\\ i& 0 \end{bmatrix}\end{array} \)
where i =√(-1), then find BA.
Solution:
Given,
\(\begin{array}{l}A=\begin{bmatrix} -i & 0\\ 0& i \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B=\begin{bmatrix} 0& i\\ i& 0 \end{bmatrix}\end{array} \)
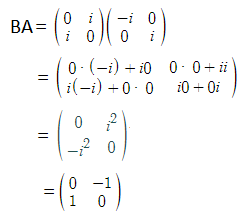
Question 2: The order of a matrix A is 3 x 4 and B is a matrix such that ATB and ABT both are defined, then find the order of B.
Solution:
Given,
Order of the matrix A = 3 x 4
∴ Order of the matrix AT = 4 x 3
Also, given that: ATB and ABT are defined.
Hence, the order of B is 3 x 4.
Question 3: If \(\begin{array}{l}A=\begin{bmatrix} -2 & -1 & 1\\ -1 & 7 & 4\\ 1 & -x & -3 \end{bmatrix}\end{array} \)
is a symmetric matrix, then find the value of x.
Solution:
Given,
\(\begin{array}{l}A=\begin{bmatrix} -2 & -1 & 1\\ -1 & 7 & 4\\ 1 & -x & -3 \end{bmatrix}\end{array} \)
A is a symmetric matrix.
Thus, aij = aji
Now,
a32 = a23
⇒ -x = 4
⇒ x = -4
Question 4: If \(\begin{array}{l}A=\begin{bmatrix} 2 & 3 & -4\\ -1 & 2 & 3 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B=\begin{bmatrix} -1 & 2\\ 3 & 4\\ -5 & -6 \end{bmatrix}\end{array} \)
, then find A + BT.
Solution:
Given,
\(\begin{array}{l}A=\begin{bmatrix} 2 & 3 & -4\\ -1 & 2 & 3 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B=\begin{bmatrix} -1 & 2\\ 3 & 4\\ -5 & -6 \end{bmatrix}\end{array} \)
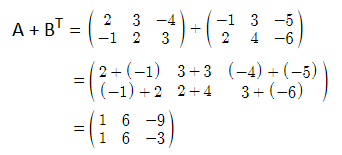
Question 5: If \(\begin{array}{l}A=\begin{bmatrix} 2 & 3\\ -1 & 4 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B=\begin{bmatrix} 1 & -1\\ 2 & 5 \end{bmatrix}\end{array} \)
, then prove that: (AB)T = BTAT
Solution:
Given,
\(\begin{array}{l}A=\begin{bmatrix} 2 & 3\\ -1 & 4 \end{bmatrix}\end{array} \)
and \(\begin{array}{l}B=\begin{bmatrix} 1 & -1\\ 2 & 5 \end{bmatrix}\end{array} \)
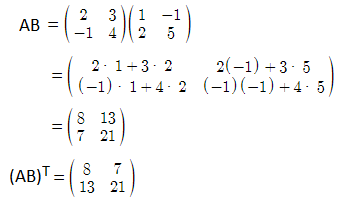
Now multiply the transpose of B and A,
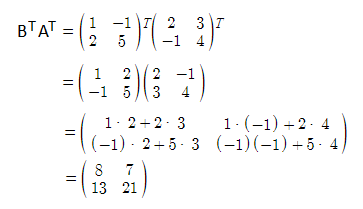
Therefore, (AB)T = BTAT
Hence proved.
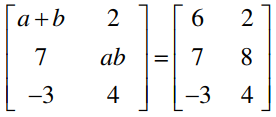
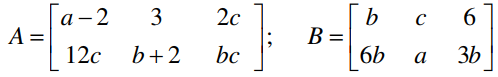
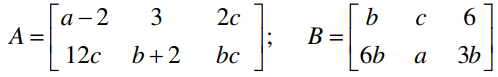
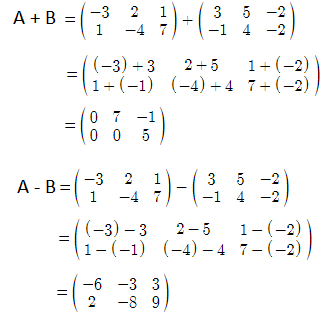

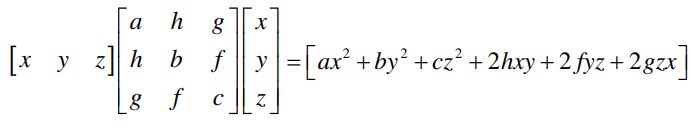
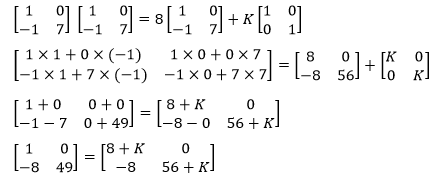
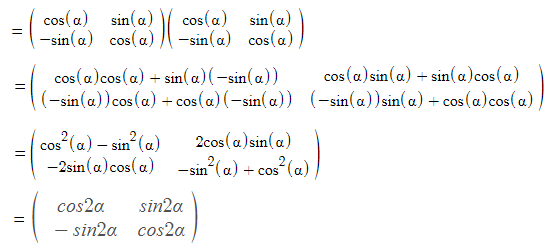
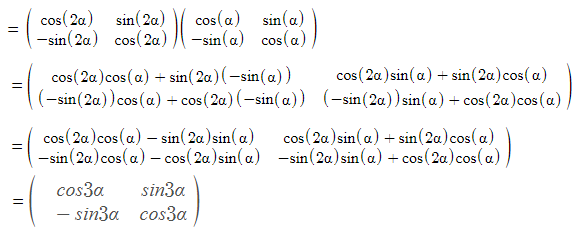
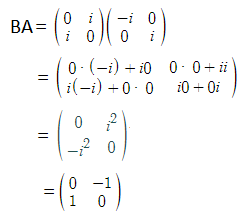
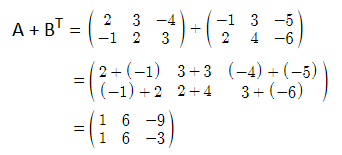
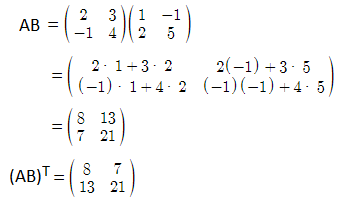
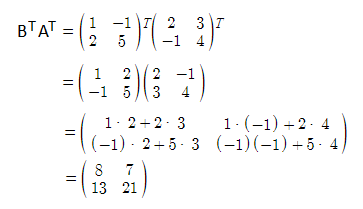
Comments