Constant Product Rule

This rule can be used when there is a relationship of inverse proportionality between two parameters, i.e. when the product of two parameters is constant. This concept can be applied to many arithmetic topics based on percentages like Time and Work, Time Speed Distance, Interest and Profit & Loss to just name a few. Please refer BYJU’S CAT College Predictor tool.

For example,

• Time x Speed = Distance
• Efficiency x Time= Work Done
• Price x Consumption = Expenditure

In the third example, if the price of a commodity is increased by a particular percentage, then to keep the “Expenditure”, which is the product of Price and Consumption constant, we need to reduce Consumption by a particular percentage.

This reduction in percentage depends entirely on the percentage by which the price has been increased. If the increase in price is 50%(1/2), then the consumption has to be decreased by 33% (1/3) to keep the expenditure constant.

Statement of Constant Product Rule:

The rule states that,

“A 1/x increase in one of the parameters will result in a 1/(x+1) decrease in the other parameter if the parameters are inversely proportional. Note that two inversely proportional quantities have a constant product also A 1/x decrease in one of the parameters will result in a 1/(x-1) increase in the other parameter if the parameters are inversely proportional. Using this concept, we can draw a table for the change in component Q reflected due to a change in component P when their product is constant, i.e when P and Q are inversely proportional.”

⇒

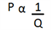
Application Based Questions On Constant Product Rule:

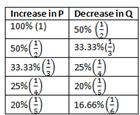
1) Price of sugar is going up by 20%. Find the percentage reduction in consumption a family should adopt so that the expenditure remains constant?

Solution:

Here price x quantity = expenditure (constant) 20 % (1/5) increase in price will result in (1/6) i.e 16.66% decrease in consumption.

2) Normally A does a certain work. But A is absent so Ravi has two options: B or C. B can finish the work by taking 6 hrs more than A while C is 1.5 times more efficient than B and can finish the work 4 hrs earlier. Find the usual time taken by A.

Solution:

Again we have two cases

Case 1 B efficiency = x 6 hrs more than A

Case 2 C efficiency = 1.5x 4 hrs less than A

Now we know efficiency and time are two inversely proportional quantities. Taking case 1 as original, efficiency increases by ½ so the time is taken will decrease by 1/3 from case1 to case 2. 6 hrs more than A and 4 hrs less than A means a difference of 10 hrs. As we have already calculated, the time taken will decrease by 1/3 and the difference is 10 hrs this means the original time taken in case 1 will be 30 hrs,

i.e. B takes 30 hours. (1/3 of 30 hrs = 10 hrs)

So time taken by A = 30-6=24 hrs.

3) An architect is planning to increase the length of a rectangular room by 10% without increasing the area of the room. By what percentage must he reduce the breadth of the room?

Solution:

Length x breadth = Area ( constant)

Since there is a 10% (1/10) increase in length the breadth will be reduced by1/11 = 9.09%.

4) Efficiency of A is 33.33% more than that of B. B takes 24 days to complete work. How many days A will take to complete the work?

Solution:

Efficiency x time = work( constant)

Efficiency of A is 33.33% (1/3) more.

So time taken by A will be 25 % less than that by B => A will take 18 days.

5) 24 men can finish work in 25 days. In how many days will 30 men finish the work?

Solution:

Here (number of men) x (number of days) = man days (constant)

By increasing the number of men by 25 %, the time saved will be 20 %. So 30 men will take 20 days to finish the work.

Till now we have discussed questions where the % change can be written as 1/x.

What if the change is not of the form 1/x? For eg = 30 % = 30/100=3/10

IF there is a 3/10 increase in one parameter, the other parameter will get reduced by 3/(10+3)=3/13

Looking at this in a table, let A ∝ 1/B i.e AB = K, a constant.

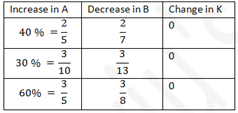
Here is an example question that illustrates the application of the constant product rule in Time Speed Distance questions.

6) A man travels from his home to the office at 4km/hr and reaches his office 20 min late. If the Speed had been 6 km/hr he would have reached 10 min early. Find the distance from his home to office?

There are 2 cases here

Case 1: Speed = 4 km/hr 20 min late

Case 2: Speed = 6 km/hr 10 min early

Step 1: Calculate the increase or decrease in the parameters Speed/Time. To calculate increase/decrease one needs to consider a case as the original case and then calculate the increase or decrease over it.

The first case can be considered as the original case, so it can be easily observed that the increase in speed is 50% or ½ from case 1 to case 2 (1/2 x100= 50%).

Step 2: Inverse Proportionality

Now based on inverse proportionality there will always be a 1/3 or 33% or decrease in Time from case 1 to case 2.

Step 3: Calculating the actual Time and the Distance

Suppose in case 1 which i.e. original one, Time taken is ‘x’ mins. So, due to ½ increase in Speed, you have 1/3 decrease in Time i.e. 1/3 of x = 30 mins. (from 20 minutes late to 10 min early there is a decrease of 30 minutes) x = 90 minutes.

So in case 1, he is taking 90 mins to travel at a speed of 4km/hr. So, Distance= 1.5 * 4 = 6 km.

To learn more about such important CAT exam topics easily, keep visiting BYJU’S. BYJU’S also provide the latest notification, pattern and syllabus of the CAT exam.