Circular Motion in a Vertical Plane:
We already have some idea about circular motion. It is a type of motion in which the distance of the body remains constant from a fixed plane. It is further classified as a uniform and non-uniform circular motion. Some examples of circular motion are a ball tied to a string and swung in a circle, a car taking a curve on a track etc. Here we will be discussing a special type of motion known as vertical circular motion.
Vertical Circular Motion Using a String
Suppose a body is tied to a string and rotated in a vertical circle as shown
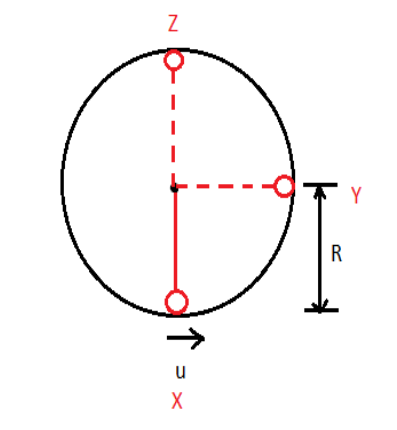
Between X and Y, tension will balance out weight and hence the string will always be taut. So the velocity required to reach Y can be found out by conserving mechanical energy,
Since the particle just reaches point Y, hence Velocity at Y is zero.
Equating both we get,
Now if I want to find the minimum velocity to reach point Z, can I assume velocity to be zero at Z? The answer is no because if the velocity is zero at Z then weight will not be balanced and the string will become slack. So at Z, velocity should be such that the weight is equal to the centripetal force, making tension just to be zero.
Substituting the value of v we get
Equating Ex and Ez we get,
So now we have our critical values we can frame our cases,
Case I:
The ball will oscillate and never reach point Y.
Case II:
The ball will lose contact somewhere between Y and Z and start projectile motion.
Case III:
The string will never become slack and complete the circle.
The situation is similar when the ball is tied to a rod and moved in a vertical circle. The only difference is now the velocity at the top can be zero. As now the normal reaction of the rod can balance the weight at that point. Solving similarly as above we get the following cases for a rod:
Case I:
The body will oscillate and not reach point Y.
Case II:
The ball will oscillate and cross point Y but not reach point Z.
Case III:
The body will complete the circle.
Recommended Video

Stay tuned with BYJU’S to learn more about laws of motion, tension and many more.


Comments