Atmospheric Pressure And Gauge Pressure

As we know, the atmospheric pressure at any point is measured as the weight of the column of air of unit cross-sectional area extended from the point under consideration to the top of the atmosphere. Using the same principle, a device was introduced by an Italian scientist Evangelista Torricelli, as shown in the figure below.

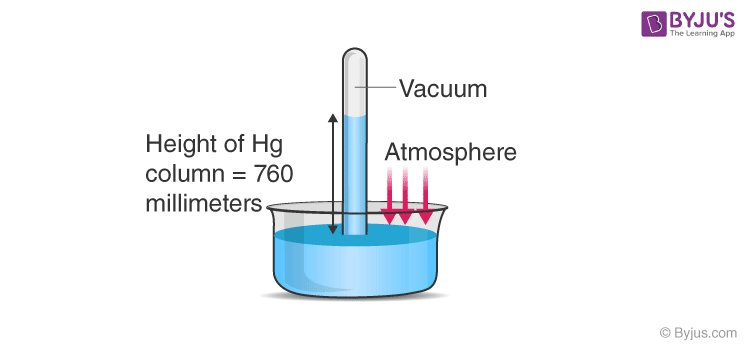
He took a long glass tube closed at one end and filled with mercury and inverted it into a trough of mercury. This device is termed as the mercury barometer. Here we can see that the space above the mercury column is filled with mercury vapours whose pressure is negligible, so it can well be considered a vacuum. Here, the pressure inside the column must be equal to the atmospheric pressure, as they are at the same level, so

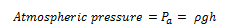
Where, h is the height of the mercury column, ρ is the density of the fluid, P_a is the atmospheric pressure and g is the acceleration due to gravity. In this experiment, the height of the mercury column was equal to 76 cm and thus, we commonly state the pressure in terms of cm or mm of mercury. An open-tube manometer, as shown above, is useful in measuring the pressure differences. It can be seen in the next apparatus as shown in the figure.

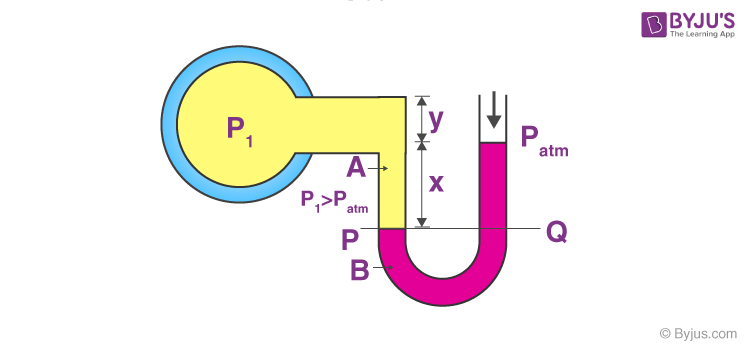
This apparatus consists of a U-tube containing a suitable liquid such as oil for measuring small pressure differences and high-density liquid for measuring large pressure differences. At one end, the tube is open to the atmosphere as can be seen in the figure and at the other end, it is connected to the system whose pressure is to be measured. The pressure P is equal to the pressure Q, as both the liquids are at the same level. What we measure usually is the gauge pressure which is equal to P-P_a, (where P_a is the atmospheric pressure), which is given by the above-stated formula of atmospheric pressure and is proportional to the height of the mercury column.

To learn more about atmospheric pressure and gauge pressure and other related topics, download BYJU’S The Learning App.