Bending Equation Derivation

Bending theory is also known as flexure theory is defined as the axial deformation of the beam due to external load that is applied perpendicularly to a longitudinal axis which finds application in applied mechanics.

For a material, flexural strength is defined as the stress that is obtained from the yield just before the flexure test. It represents the highest stress that is experienced within the material at the moment of its yield. 𝜎 is used as the symbolic representation of flexural strength.

Bending Equation derivation

Following are the assumptions made before the derivation of the bending equation:

  • The beam used is straight with a constant cross-section.
  • The beam used is of homogeneous material with a symmetrical longitudinal plane.
  • The plane of symmetry has all the resultant of applied loads.
  • The primary cause of failure is buckling.
  • E remains the same for tension and compression.
  • Cross-section remains the same before and after bending.

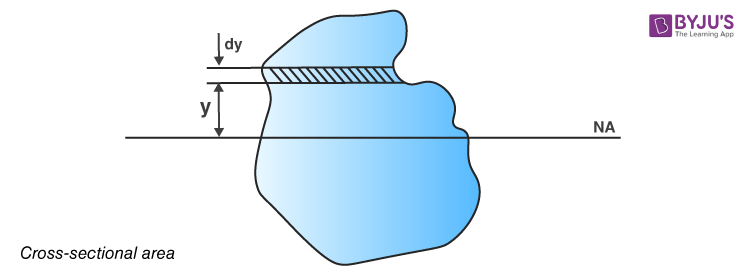
Consider an unstressed beam, which is subjected to a constant bending moment such that the beam bends up to radius R. The top fibres are subjected to tension whereas the bottom fibres are subjected to compression. The locus of points with zero stress is known as the neutral axis.

Read More: Young’s Modulus

Bending Theory Diagrams

With the help of the above figure, the following are the steps involved in the derivation of the bending equation:

Strain in fibre AB is the ratio of change in length to original length.

Strain in fibre

\(\begin{array}{l}AB=\frac{{A}'{B}’-AB}{AB}\end{array} \)
\(\begin{array}{l}∴ strain=\frac{{A}'{B}’-{C}'{D}’}{{C}'{D}’}\end{array} \)
(as AB = CD and CD = C’D’)

CD and C’D’ are on the neutral axis and stress is assumed to be zero, therefore strain is also zero on the neutral axis.

\(\begin{array}{l}=\frac{(R+y)\Theta -R\Theta }{R\Theta }\end{array} \)
\(\begin{array}{l}=\frac{R\Theta +y\Theta -R\Theta }{R\Theta }\end{array} \)
\(\begin{array}{l}=\frac{y}{R}\end{array} \)
\(\begin{array}{l}\frac{\sigma }{E}=\frac{y}{R}\end{array} \)
where E is Young’s Modulus of Elasticity

Or

\(\begin{array}{l}\frac{\sigma }{y}=\frac{E}{R}\end{array} \)

\(\begin{array}{l}\sigma =\frac{E}{R}y\end{array} \)
(eq.1)

\(\begin{array}{l}F=\sigma \delta A=\frac{E}{R}y\delta A\end{array} \)
(force acting on the strip with area dA)

\(\begin{array}{l}Fy=\frac{E}{R}y^{2}\delta A\end{array} \)
(momentum about neutral axis)

\(\begin{array}{l}M=\sum \frac{E}{R}y^{2}\end{array} \)
(total momentum for entire cross-sectional area)

\(\begin{array}{l}\delta A=\frac{E}{R}\sum y^{2}\delta A\end{array} \)
\(\begin{array}{l}\sum y^{2}\delta A\end{array} \)
is known as the second momentum of the area and is represented as I.

\(\begin{array}{l}∴ M=\frac{E}{R}I\end{array} \)
(eq.2)

From eq.1 and eq.2 we get,

\(\begin{array}{l}\frac{\sigma }{y}=\frac{M}{I}=\frac{E}{R}\end{array} \)

Therefore, the above is the bending theory equation.

Related Physics articles:

Faraday’s Law Electromagnetic Induction

Does light take the quickest path?

Stay tuned with BYJU’S for more such interesting articles. Also, register to “BYJU’S – The Learning App” for loads of interactive, engaging Physics-related videos and an unlimited academic assist.

Test your knowledge on Bending equation derivation
Quiz Image

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz

Congrats!

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

0 out of 0 arewrong
0 out of 0 are correct
0 out of 0 are Unattempted
PHYSICS Related Links
Thrust Physics About Indian Scientists And Their Inventions
What Is Carnot Engine Calorimeter Definition
What Is Photodiode Transverse Motion
Optics Definition Groundwater Recharge
Disaster Management Project Class 9 Earthquake What Is Meant By Velocity

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*