Equation of Motion and Its Application

Introduction to Equations Of Motion

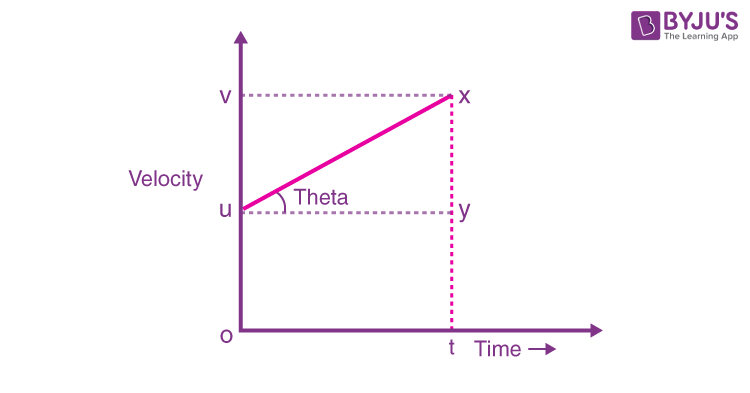
In this article, we will learn how we can relate quantities like velocity, time, acceleration and displacement provided the acceleration remains constant. These relations are collectively known as the equation of motion. There are three equations of motion. There are three ways to derive the equation of motion and here we are going to derive with the help of a graph.

Read More: Derivation of Equation of Motion

First Equation of Motion

First equation of motion relates velocity, time and acceleration. Now in ∆uxy,

\(\begin{array}{l}tanθ = \frac {xy}{uy}\end{array} \)

 

\(\begin{array}{l}tanθ = \frac {v~-~u}{t}\end{array} \)

 
We also know that tanθ is nothing but the slope, and slope of the v – t graph represents acceleration.

⇒ v = u + at ———– (1)

This is the first equation of motion where,

v = final velocity

u = initial velocity

a = acceleration

t = time taken

Second Equation of Motion

Now coming to the second equation of motion, it relates displacement, velocity, acceleration and time. The area under the v – t graph represents the displacement of the body.

In this case,

Displacement = Area of the trapezium (ouxt)

\(\begin{array}{l}S = \frac 12 \,\, \times \textup{ sum of parallel sides } \times \,\, height\end{array} \)

 

\(\begin{array}{l}S = \frac 12 \,\, \times \textup{ (v + u) } \times \textup{ t ——— (2)} \end{array} \)

 
We can substitute v in terms of others and get the final equation as:

\(\begin{array}{l}S = ut + \frac 12~ at^2\end{array} \)

 
Where symbols have their usual meaning.

Third Equation of Motion

The third equation of motion relates to velocity, displacement, and acceleration. Using the same equation (2),

\(\begin{array}{l} S = \frac 12 \,\, \times \textup{ (v + u) } \times \textup{ t} \end{array} \)

 
Using equation (1), if we replace t, we get,

\(\begin{array}{l}S = \frac 12  \times (v + u) \times \frac{(v-u)}{a}\end{array} \)

 

\(\begin{array}{l}S = \frac {(v^2~-~ u^2)}{2a}\end{array} \)

 

\(\begin{array}{l} v^2  =  u^2~ +~ 2as\end{array} \)

 
The above equation represents our third equation of motion.

Read More: Displacement

Applications of Equations of Motion

So now that we have seen all three equations of motion, we can use them to solve kinematic problems. We just have to identify what all parameters are given and then choose the appropriate equation and solve for the required parameter.

The equations of motion are also used in the calculation of optical properties.

The Fundamentals of Motion: Understanding the Laws of Physics

Frequently Asked Questions – FAQs

Q1

What is motion?

Motion is the phenomenon in which an object changes its position.

Q2

What is the first equation of motion?

The first equation of motion is given as:
v = u + at
Where,
v = final velocity
u = initial velocity
a = acceleration
t = time taken

Q3

What is the second equation of motion?

The second equation of motion is given as:

\(\begin{array}{l}S = ut + \frac 12~ at^2\end{array} \)

Where,
v = final velocity
u = initial velocity
a = acceleration
t = time taken

Q4

What is the third equation of motion?

The third equation of motion is given as:

\(\begin{array}{l}v^2 = u^2~ +~ 2as\end{array} \)

Where,
v = final velocity
u = initial velocity
a = acceleration
t = time taken

Q5

What does the area under the v – t graph represent?

The area under the v – t graph represents the displacement of the body.

Important questions in the chapter Motion Class 9

Top 10 NTSE Important Questions on Motion Class 9

To learn more related concepts with the help of interactive video lessons, download BYJU’S – The Learning App.