As we know, many forms of energy like light and sound travel in waves. A wave is defined through various characteristics like frequency, amplitude and speed. In wave mechanics, any given wave enfolds parameters like – frequency, time period, wavelength, amplitude etc. This article lets us understand and learn in detail about frequency, time period, and angular frequency.
| Table of Contents: |
Parameters of a Wave
Frequency definition states that it is the number of complete cycles of waves passing a point in unit time. The time period is the time taken by a complete cycle of the wave to pass a point. Angular frequency is angular displacement of any element of the wave per unit of time.
Consider the graph shown below. It represents the displacement y of any element for a harmonic wave along a string moving in the positive x-direction with respect to time. Here, the string element moves up and down in simple harmonic motion.
Read More: Angular Displacement
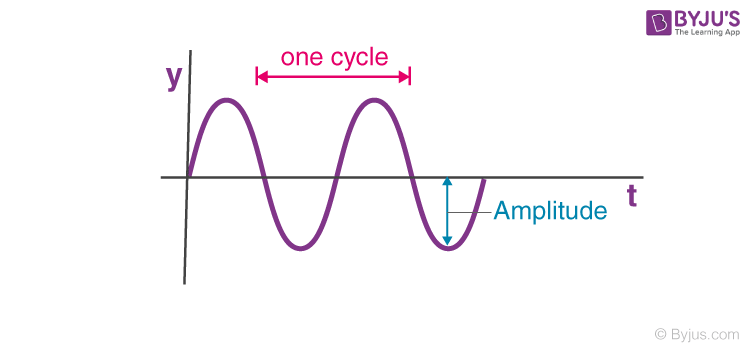
The relation describing the displacement of the element with respect to time is given as:
y (0,t) = a sin (–ωt), here we have considered the inception of wavefrom x=0
y (0,t) = -a sin (ωt)
As we know, sinusoidal or harmonic motion is periodic in nature, i.e. the nature of the graph of an element of the wave repeats itself at a fixed duration. To mark the duration of periodicity following terms are introduced for sinusoidal waves.
Following is the table explaining other related concepts of waves:
| Introduction to Periodic Motion |
| Speed of Wave Motion |
| Simple Harmonic Motion |
What Is Time Period?
As shown above, the particles move about the mean equilibrium or mean position with time in a sinusoidal wave motion. The particles rise until they reach the highest point, the crest, and then continue to fall until they reach the lowest point, the trough. The cycle repeats itself in a uniform pattern. The time period of oscillation of a wave is defined as the time taken by any string element to complete one such oscillation. For a sine wave represented by the equation:
y (0, t) = -a sin(ωt)
The time period formula is given as:
\(\begin{array}{l}T=\frac{2\pi }{\omega }\end{array} \) |
What Is Frequency?
We define the frequency of a sinusoidal wave as the number of complete oscillations made by any wave element per unit of time. By the definition of frequency, we can understand that if a body is in periodic motion, it has undergone one cycle after passing through a series of events or positions and returning to its original state. Thus, frequency is a parameter that describes the rate of oscillation and vibration.
The equation gives the relation between the frequency and the period:
The relation between the frequency and the period is given by the equation:
f=1/T
For a sinusoidal wave represented by the equation:
y (0,t) = -a sin (ωt)
The formula of the frequency with the SI unit is given as:
| Formula | \(\begin{array}{l}f=\frac{1}{T}=\frac{\omega }{2\pi }\end{array} \) |
| SI unit | Hertz |
One Hertz is equal to one complete oscillation taking place per second.
What Is Angular Frequency?
For a sinusoidal wave, the angular frequency refers to the angular displacement of any element of the wave per unit of time or the rate of change of the phase of the waveform. It is represented by ω. Angular frequency formula and SI unit are given as:
| Formula | \(\begin{array}{l}\omega=\frac{2\pi }{T}=2\pi f\end{array} \) |
| SI unit | rads-1 |
Where,
- ω = angular frequency of the wave.
- T = time period of the wave.
- f = ordinary frequency of the wave.
Here is a video for you which demonstrates the time period, frequency and wavelength of a sound wave
Frequently Asked Questions – FAQs
What is a wave?
What is the formula to find the frequency?
Define Frequency.
Define Time Period.
Define Angular Frequency.
Angular Velocity: Where did it come from, who thought about it and why?
Stay tuned to BYJU’S and Fall in Love with Learning!
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
thanks for the simple answer