Distance and displacement are two quantities that seem to mean the same but are distinctly different with different meanings and definitions. Distance is the measure of “how much ground an object has covered during its motion” while displacement refers to the measure of “how far out of place is an object.” In this article, let us understand the difference between distance and displacement.
| Table of Contents: |
What Is Distance?
Distance is the total movement of an object without any regard to direction. We can define distance as to how much ground an object has covered despite its starting or ending point.
Let’s understand the concept of distance with the help of the following diagram:
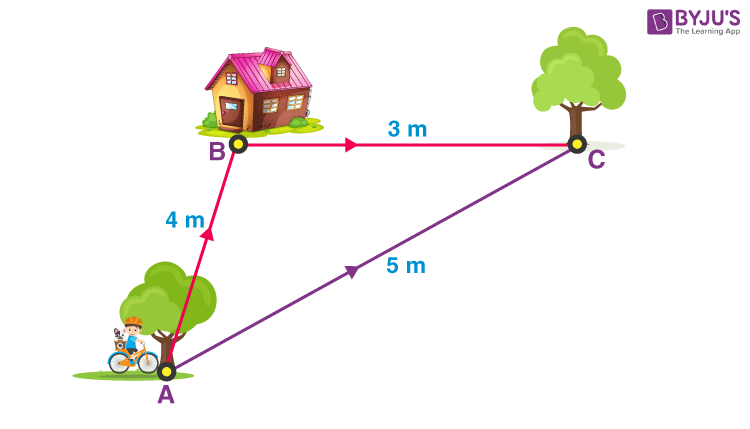
Explanation of distance
Distance here will be = 4m + 3m + 5m = 12 m
Distance Formula
How is Displacement defined?
Displacement =
The below video provides an overview of the measurement of motion
Examples ofΒ Distance and Displacement
Question 1. John travels 250 miles to North but then back-tracks to South for 105 miles to pick up a friend. What is Johnβs total displacement?
Answer: Johnβs starting positionΒ Xi= 0.
Her final position Xf is the distance travelled N minus the distance South.
Calculating displacement, i.e.D.
D = ΞX = (Xf – Xi)
D = (250 mi N – 105 mi S) – 0
D = 145 mi N
Question 2.Β An object moves along the grid through points A, B, C, D, E, and F as shown below. The side of square tiles measures 0.5 km.
a) Calculate the distance covered by the moving object.
b) Find the magnitude of the displacement of the object.
Solution:
a) The distance covered by the moving object is calculated as follows:
AB + BC + CD + DE + EF
3 + 1 + 1.5 + 0.5 + 0.5 = 6.5 km
The distance covered by the moving object is 6.5 km.
b) The initial point is A and the final point is F, hence the magnitude of the displacement is equal to the distance AF which is calculated by applying Pythagoras’s theorem to the triangle AHF as shown in the figure below
Applying the Pythagorean formula, we get
Substituting the formula, we get
The magnitude of displacement is 2.5 km.
Distance vs Displacement
| Distance | Displacement |
| The complete length of the path between any two points is called distance | Displacement is the direct length between any two points when measured along the minimum path between them |
| Distance is a scalar quantity as it only depends upon the magnitude and not the direction | Displacement is a vector quantity as it depends upon both magnitude and direction |
| Distance can only have positive values | Displacement can be positive, negative and even zero |
Read More: Difference Between Distance and Displacement
Watch the video and understand how is motion different from rest!
We at BYJU’S, strongly believe that a spirit of learning and understanding can only be inculcated when students are curious, and that curiosity can be brought about by creative and effective teaching. This approach makes our lectures so successful and gives our students an edge over their counterparts.
Frequently Asked Questions β FAQs
Can the distance be negative?
Is displacement a scalar or vector quantity?
Displacement is a vector quantity since it has both magnitude and direction.
Can displacement be zero?
Yes, displacement can be zero.
What is meant by distance?
What is meant by displacement?
Put your understanding of this concept to test by answering a few MCQs. Click βStart Quizβ to begin!
Select the correct answer and click on the βFinishβ button
Check your score and answers at the end of the quiz
Visit BYJUβS for all Physics related queries and study materials
Your result is as below
I learned about the distance of feet and miles.
Very helpful for study. Thank you BYJU’S
Thank You BYJU’S !~