Drift refers to the slow movement towards a thing/object. The average velocity of charged particles in a material due to an electric field is known as drift velocity. In this session, let us learn in detail about drift velocity.
| Table of Contents: |
What is Drift Velocity?
Subatomic particles like electrons move in random directions all the time. When electrons are subjected to an electric field they do move randomly, but they slowly drift in one direction, in the direction of the electric field applied. The net velocity at which these electrons drift is known as drift velocity.
Drift velocity can be defined as:
The average velocity attained by charged particles, (eg. electrons) in a material due to an electric field.
The SI unit of drift velocity is m/s. It is also measured in m2/(V.s).
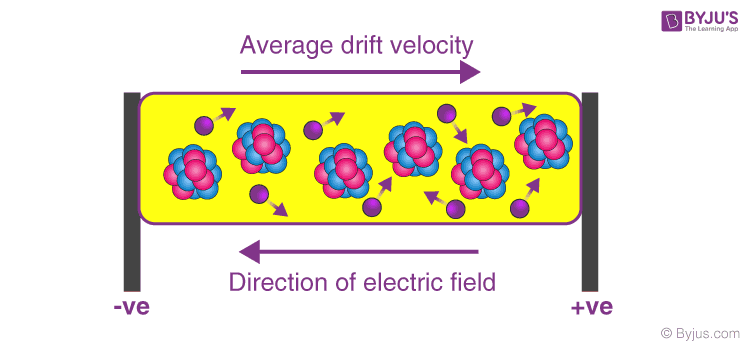
Net velocity of the electrons:
Every material above absolute zero temperature which can conduct like metals will have some free electrons moving at random velocity. When a potential is applied around a conductor the electrons will tend to move towards the positive potential, but as they move, they will collide with atoms and will bounce back or lose some of their kinetic energy. However, due to the electric field, the electrons will accelerate back again, and these random collisions will keep happening but as the acceleration is always in the same direction due to the electric field, the net velocity of the electrons will also be in the same direction.
You may also want to check out these topics given below!
- Derivation of Drift Velocity
- Relationship Between Escape and Orbital Velocity
- Relative Motion and Relative Velocity
Formula To Calculate Drift Velocity
We can use the following formula in order to calculate drift velocity:
\(\begin{array}{l} I = nAvQ \end{array} \) |
Where,
- I is the current flowing through the conductor which is measured in amperes
- n is the number of electrons
- A is the area of the cross-section of the conductor which is measured in m2
- v is the drift velocity of the electrons
- Q is the charge of an electron which is measured in Coulombs
The video about current electricity Class 12 Physics
Example:
Let’s consider a current of 3A that is flowing in a copper conductor with a cross-section of 1mm2 (1×10-6m2)
We know that for copper, n = 8.5 x 1028 per m3
So according to the formula we have,
Where,
Therefore,
If the intensity of the electric field is increased then the electrons are accelerated more rapidly towards the positive direction, opposite to the direction of the electric field applied.
Mobility of an electron:
The drift velocity of an electron for a unit electric field is known as mobility of the electron.
Mobility of an electron can be calculated by:
\(\begin{array}{l} \mu = \frac {V_d}{E} \end{array} \) |
Relation between Drift Velocity and Electric Current
Mobility is always a positive quantity and depends on the nature of the charge carrier, the drift velocity of an electron is very small usually in terms of 10-3ms-1. Hence, at this velocity it will take approx. 17 mins for electrons to pass through a conductor of 1 meter. But, surprisingly, we can turn on electronic appliances in our home at lightning speeds with a flick of a switch this is because an electric current is not established with the drift velocity but with the speed of light.
As soon as the electric field is established the current starts flowing inside the conductor at the speed of light and not at the speed at which the electrons are drifting, hence there is a negligible small delay between an input and an output in turning on of an electric bulb.
Relation between Drift Velocity and Current Density
We can define current density as the total amount of current passing through a unit cross-sectional conductor in unit time. From drift velocity, we know the formula for drift velocity as:
I = nAvQ
J = I/A = nVQ
Where,
- J is the current density measured in Amperes per square meter
- v is the drift velocity of the electrons
Thun, we can say that the drift velocity of the electrons and their current density are directly proportional to each other. Also, when the electric field intensity increases, the drift velocity increases and the current flowing through the conductor also increases.
See the video below to learn about the current electricity, drift velocity, and mobility for JEE syllabus
Frequently Asked Questions – FAQs
What is meant by velocity?
Velocity is the rate at which bodies change their position relative to a frame of reference (rate change of position). Velocity can be described as the pair of a body’s speed and direction of propagation.
What is meant by drift velocity?
It is the average velocity acquired by a charged particle (like an electron or proton) in the body due to an electric field. Usually, an electron inside a conductor moves arbitrarily at the Fermi velocity, generating a zero average velocity.
What is meant by electron mobility?
What is the formula to find the drift velocity?
I = nAvQ
Here,
I – the current flowing through the conductor
n – the number of electrons
A – the area of the cross-section of the conductor
v – the drift velocity of the electrons
Q – the charge of an electron
What are the characteristics of drift velocity?
When an electric field is exerted over a conductor, the electrons jump towards the high potential terminal of the given wire.
Unless an electric field is offered to the conductor, the internal electrons move at arbitrary velocities and directions.
The current moving inside a conductor is directly proportional to the electrons’ drift velocity.
If you wish to learn more Physics concepts with the help of interactive video lessons, download BYJU’S – The Learning App.
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Thank you so much it was very helpful.
Thanks a lot for this quiz questions