A pulley is a wheel that bears a cord, chain, cable, belt or flexible rope on its rim. It is used to transmit motion and energy. In this article, we will go into the concepts of pulley systems.
| Table of Contents |
Pulley System
The Pulley System makes use of a disk-shaped block that a rope wraps around to create a simple machine. The tension force that is applied on one side of the rope uses the pulley system to divert the force in a different direction. Most of the examples in our NCERT books are ideal machines in which no force is lost due to friction or any other factors. Some of these parameters are established and mentioned below:
- The magnitude of the applied force does not change, but the direction does as the pulley be considered as a perfect simple machine. The resistance that the pulley provides to the rope is zero.
- One does not need to worry about the rope and pulley’s energy when applying the Law of Conservation of energy.
- When the force’s effect on the body attached to the pulley is calculated, the pulley’s mass need not be considered.
The video below gives you an insight into how to solve problems related to pulley systems.

Pulleys – Their Purpose
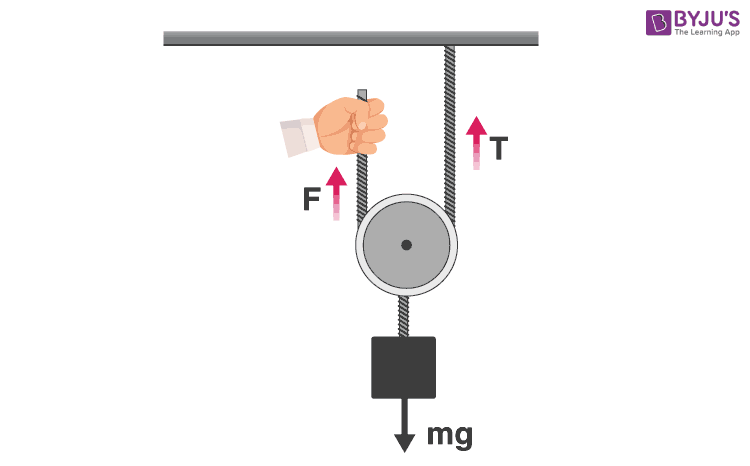
The force that needs to be exerted gets reduced when using the pulley to lift bodies. For instance, at a mass hanging from the pulley, a force F is applied. You will notice that the force normally required for lifting that amount of mass will be more than the force F that was applied to the pulley system.
In a normal situation, to lift a mass m with a velocity that’s constant without the use of a pulley a force is applied that is equal to the mass of the object suspended from the string. The force will be represented as mg i.e. mass multiplied by gravity. By making use of a pulley this mass will also be lifted with a force of mg along with tension (t) in an upward direction. The force gets dispersed amongst the tension of the rope fixed to the ceiling, T, and the tension of the rope wrapped up in your hand, F.
The block of mass (m) is pulled upwards by two forces of F and T. We know that mg will be equivalent to F + T and thus
2F = mg or F = mg/2
Thus, we are left with the concept that only half the force will be required to lift a weight of mg. This is the use of a simple machine more specifically, a pulley.
Here is a problem based on the weighing machine, the problem deals with an advanced question on how normal reaction and tension act in an accelerated pulley system when the support is provided by the man which is being measured.

Watch the video to and learn to solve pulley problems using constraint equations.

Stay tuned with BYJU’S for more such interesting articles. Also, register to “BYJU’S – The Learning App” for loads of interactive, engaging Physics-related videos and unlimited academic assistance.
Frequently Asked Questions – FAQs
What is a pulley?
A pulley is a type of wheel that is on a shaft or wheel. It is designed to change the direction and movement of a taut belt or cable. It can also be used to transfer power between the belt or cable and the shaft.
What are the main components of a pulley?
A simple pulley mainly consists of a wheel, hook, flexible belt and axle.
What are the three main types of pulleys?
Compound, fixed and movable pulleys are the three main types of pulleys.
What are the main uses of pulleys?
Pulleys are typically utilised in shipping, industrial equipment and other heavy machinery. These mechanical systems use one or more pulleys to enhance mechanical working as it decreases the force required to pull or lift the weight.
What is a simple machine?
A simple machine is a basic tool that varies the magnitude or direction of a force. It utilises the simplest mechanism to multiply force.
What are the important examples of simple machines?
Pulley, screw, lever, wheel and axle, inclined plane, and wedge are important examples of simple machines.
Which is the oldest simple machine?
The wedge is the oldest simple machine.

Comments