CAT 2023 study materials: The candidates appearing in the upcoming exam must follow the experts’ recommended CAT study material to cover all three exam sections. Choosing the best CAT preparation material should be your responsibility, as there are many books and study materials to prepare for CAT exam. The CAT study material mainly includes books, study notes, previous years’ questions, chapter-wise exercises, sectional tests and mock tests. Please refer BYJU’S CAT College Predictor tool.
The CAT exam is one of the most competitive exams in India. It is taken by almost over a quarter of a million MBA aspirants every year. The exam is a prerequisite for admissions to IIMs and several other top MBA colleges in India. To ace such a competitive exam, it is extremely important to be well-equipped with proper CAT study material and prepare effectively for the exam.
Ultimate Guide to Kickstart your CAT Exam Preparation
Download the e-book now
Read the article below to know more details about CAT Study Material, important books, video materials, sample papers and last years’ exam papers.
CAT Study Material 2023 At BYJU’S
Visit the following links to get various free CAT preparation materials and preparation tips for efficient exam preparation. The CAT exam materials available at BYJU’S are given in an engaging and easy-to-understand manner to help the CAT aspirants learn in a better way.
| Important CAT Study Material | |
| CAT Preparation Books | CAT Quantitative Aptitude |
| CAT Verbal Ability | CAT Reading Comprehension |
| CAT Logical Reasoning | CAT Data Interpretation |
CAT Study Material – Video Analysis
Check these CAT video materials to understand certain CAT exam topics thoroughly. BYJU’S uses 3D animations and in-air projections to make the learners visualise the topics and retain the concepts for longer
Quadratic Equations
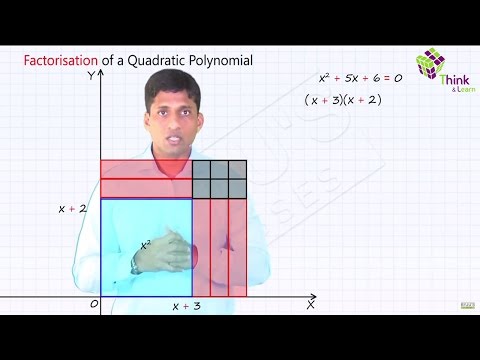
Lines and Angles
BYJU’S CAT Preparation Material – Sample Questions and Tests
We at BYJU’S also provide several CAT sample papers and previous years’ question papers for practice. Apart from the practice questions, the CAT aspirants are also provided with CAT mock tests to help them get acquainted with the actual exam scenario.
| CAT Study Material – Important PDF |
| CAT Sample Papers |
| CAT Mock Tests |
| CAT Question Papers |
These comprehensive CAT study materials will be extremely helpful in preparing effectively and acing the CAT easily. Keep visiting BYJU’S to get more such CAT preparation materials and be confident to tackle any difficult question in the exam.
CAT Free Study Material 2023
With more than 100 chapter-wise and sectional assessments and more than 25 national mock exams, this bundle provides focused practice. With a thorough examination of each test, you will discover your areas of strength and weakness. The course offers a national percentile prediction so you may assess how well you performed in relation to other candidates nationwide. In addition to test preparation, this package contains 75+ recorded video lectures and tutorials that will help you better understand a variety of topics.
CAT Exam Study Material – Previous Years’ Question PDF Download
The previous years’ questions are the best CAT study material and help the candidates to know the actual test structure, difficulty level, weightage and more. The candidates must practice previous years’ papers as many times as they can after completing the CAT syllabus in an exam-like environment. Always maintain track of your preparation after solving each question paper and know how much you are prepared for the upcoming CAT 2023.
In the section below, we have shared last years’ exam paper PDF for your reference.
- CAT 2022 Question Paper PDF Download
- CAT 2021 Question Paper PDF Download
- CAT 2020 Question Paper PDF Download
- CAT 2019 Question Paper PDF Download
- CAT 2018 Question Paper PDF Download
- CAT 2017 Question Paper PDF Download
Tips to Choose the Best CAT Study Materials
There are plenty of CAT exam study materials that are available to choose from. Before choosing any CAT preparation material, check if the materials meet the challenge of changing times. Check for the following conditions before choosing:
- The CAT study material should include content that is updated regularly and is designed on the lines of CAT and other premier examinations and ensure the learner sticks to the relevant topics. The materials or a book for CAT should ideally contain concepts explained in detail, followed by practice questions, both solved and unsolved.
- It should contain detailed solutions for all practice questions so that the learners are able to get their doubts clarified.
- It should also have section test booklets for each subject.
Why Choose BYJU’S CAT Study Material?
The courses are created taking into account the requirements of the various categories of candidates. The following are the key justifications for selecting BYJU’S CAT study material:
- Created by professionals with backgrounds from major institutions and schools, including IIMs
- Experienced instructors participate in interactive live classes employing a novel academic delivery model.
- Specific Questions Sessions in line with Concept Classes
- Toppers, IIM alumni, and industry professionals offer exclusive live discussions on exam strategy and tips.
- AI Test Analytics and self-evaluation-based Mocks provide 24×7 question clarification and discussion services.
All these conditions are met by BYJU’S study materials for CAT, as the CAT aspirants are provided with all suitable materials as detailed above.
Comment below if you have any CAT-related queries and get them resolved at the earliest. Stay tuned to BYJU’S for complete CAT 2023 assistance.