We know there are two types of lens: concave lens, and convex lens. These lenses are used as per the requirement and play an important role in the study of optics. Lens formula is a well-designed formula that is applicable for concave as well as convex lenses. The lens formula is used to find image distance, type of image formed, and the focal length (f). Let us know the derivation of the lens formula.
| Table of Contents: |
What is Lens Formula?
In optics, the relationship between the distance of the image (v), the distance of the object (u), and the focal length (f) of the lens is given by the formula known as the Lens formula. The Lens formula is applicable for convex as well as concave lenses. These lenses have negligible thickness. The formula is as follows:
Lens Formula Derivation
Consider a convex lens with an optical centre O. Let F be the principle focus and f be the focal length. An object AB is held perpendicular to the principal axis at a distance beyond the focal length of the lens. A real, inverted magnified image A’B’ is formed as shown in the figure.
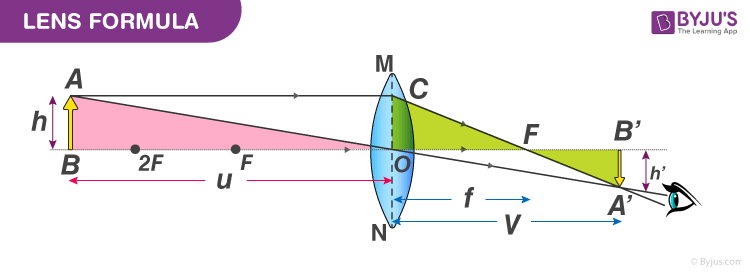
From the given figure, we notice that △ABO and △A’B’O are similar.
Therefore,
Similarly, △A’B’F and △OCF are similar, hence
But,
Hence,
Equating eq (1) and (2), we get
Substituting the sign convention, we get
OB=-u, OB’=v and OF=f
Dividing both the sides by uvf, we get
The above equation is known as the Lens formula.
This was the derivation of the Lens formula. Stay tuned with BYJU’S and learn various other Physics related topics.
Related Physics articles:
| Lenses In Optics | Concave Mirrors And Convex Mirrors |
| Uses Of Spherical Mirror: Concave And Convex Mirror | Light Sources |
See the video below, to understand the lens formula, magnification, and power.
Frequently Asked Questions – FAQs
What is a convex lens?
The convex lens is a type of lens that is thicker at the centre and gets thinner as we move towards the edges.
What is a concave lens?
The concave lens is thinner at the centre and gets thicker as we move towards the edges.
Which type is used in cameras because it focuses light and produces a clear and crisp image.?
Write lens formula?
State true or false: Lens formula is applicable for convex as well as concave lenses.
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments