It is to be noted that the charged bodies in a system of charges that are very small as compared to the distance between them are treated as point charges. In such bodies, all the charges distributed over the surface of the object are assumed to be concentrated at one point. Very often, we get to deal with systems where the influence of many such systems has to be taken into consideration. In order to calculate the final effect in such cases, we need to add and subtract these charges from one another. In order to simplify the operations involved, it is necessary to study the properties of point charges. In this section, we will learn about three such properties of point charges; the additivity of electric charge, the conservation of electric charge, and the quantization of electric charge.
| Table of Contents |
Additivity of Electric Charge
Let us consider a system of charges containing three point charges with magnitudes q1, q2, and q3. In such a system, the total charge of the system can be obtained by algebraically adding the three charges.
These charges have magnitude but no direction, are scalar quantities, and are treated like real numbers during conducting any operation. For a system containing n particles, the total charge of the system can be written as,
We note that the charge can either be positive or negative and the operation takes the sign of the charge into consideration.
Conservation of Electric Charge
According to the principle of conservation of charges, the charges are neither created nor destroyed; they are only transferred from one body to the other. For example, when two objects, one has some charge and the other having no charge are made to come in contact with each other, the charge is transferred from the object possessing some charge to the object possessing no charge until the charge is equally distributed over the whole system. Here, no charge is created or lost and is only transferred from the one possessing an excess of charge to the other possessing a deficit.
Quantization of Electric Charge
According to the principle of quantization of electric charge, all the free charges are integral multiples of a basic predefined unit, which we denote by e. Thus, the charge possessed by a system can be given as,
Where n is an integer (zero, a positive or a negative number) and e is the basic unit of charge, that is, the charge carried by an electron or a proton. The value of e is 1.6 × 10-19C.
Frequently Asked Questions – FAQs
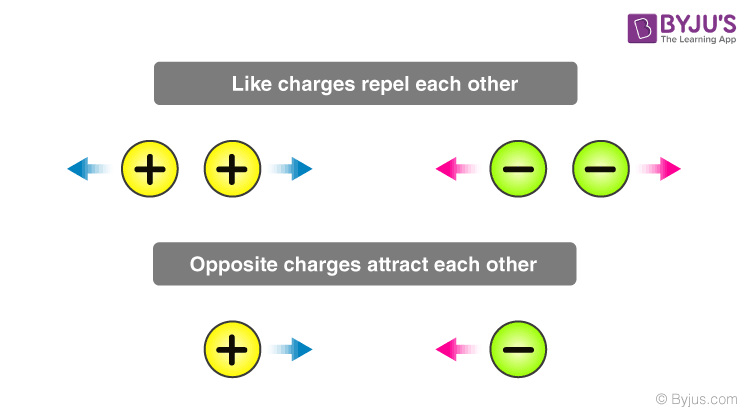
What are the types of electric charges?
- Positive (+) charge
- Negative (-) charge
What is electric charge?
What are the 2 properties of electric charge?
- (Electric charge is additive in nature.
- Conservation of electric charge.
What is the SI unit of electric charge?
Who discovered electric charge?
To learn more about the basic properties of electric charge and other related topics, download BYJU’S – The Learning App.
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments