Einstein Field Equation

What is Einstein Field Equation?

The Einstein Field Equation (EFE) is also known as Einstein’s equation. There are ten nonlinear partial differential equations of Einstein field extracted from Albert Einstein’s General Theory of Relativity. The EFE describes the basic interaction of gravitation. The equations were first published in 1915 by Albert Einstein as a tensor equation.

Following is the Einstein Field Equation:

\(\begin{array}{l}G_{\mu \upsilon } + g_{\mu \upsilon }\Lambda = \frac{8 \pi G}{c^{4}}T_{\mu \upsilon }\end{array} \)

Where,

  • Gμ𝜐 is the Einstein tensor which is given as Rμ𝜐-(½ × Rgμ𝜐)
  • Rμ𝜐 is the Ricci curvature tensor
  • R is the scalar curvature
  • gμ𝜐 is the metric tensor
  • 𝚲 is a cosmological constant
  • G is Newton’s gravitational constant
  • c is the speed of light
  • Tμ𝜐 is the stress-energy tensor
Einstein Field Equation

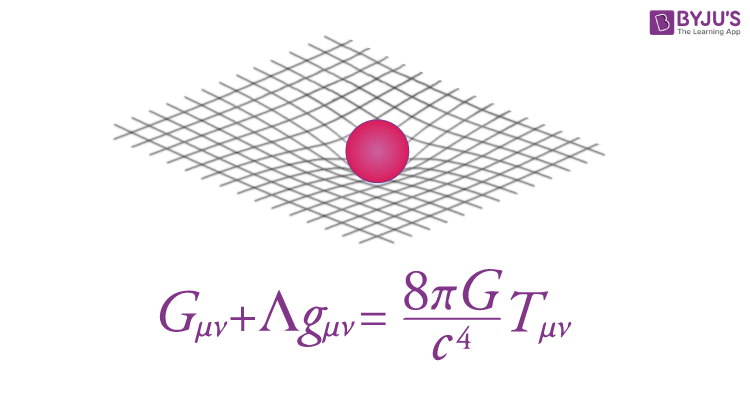
Einstein Field Equations Derivation

Following is the derivation of Einstein Field Equations. Einstein wanted to explain that measure of curvature = source of gravity.

The source of gravity is the stress-energy tensor. The stress-energy tensor is given as:

\(\begin{array}{l}T^{\alpha \beta }=\begin{bmatrix} \rho & 0 &0 & 0\\ 0&P &0 &0 \\ 0 &0 &P &0 \\ 0&0 &0 &P \end{bmatrix}\rightarrow \begin{bmatrix} \rho &0 &0 &0 \\ 0& 0 &0 &0 \\ 0 & 0& 0& 0\\ 0& 0 &0 &0 \end{bmatrix}\end{array} \)

In the above matrix we see that the P is tending to zero because, for Newton’s gravity, the mass density is the source of gravity.

The equation of motion is given as:

\(\begin{array}{l}\frac{du^{i}}{d\tau }+\Gamma _{v\alpha }^{i}u^{v}u^{\alpha }=0\end{array} \)

\(\begin{array}{l}\frac{du^{i}}{d\tau }+\Gamma _{i}^{00}=0\end{array} \)

\(\begin{array}{l}\frac{du^{i}}{d\tau }+\frac{1}{2}\frac{\partial g_{00}}{\partial x^{i}}=0\end{array} \)

\(\begin{array}{l}\frac{du^{i}}{d\tau }+\frac{\partial \phi }{\partial x^{i}}=0\end{array} \)

\(\begin{array}{l}g_{00}=-(1+2\phi )\end{array} \)

But we know that

\(\begin{array}{l}\bigtriangledown ^{2}\phi =4\pi G\rho\end{array} \)

Therefore, 

\(\begin{array}{l}R^{\mu v}=-8\pi GT^{\mu v}\end{array} \)

Where

\(\begin{array}{l}-8\pi GT^{\mu v}\end{array} \)
is the constant.

What is Einstein Tensor?

Einstein tensor is also known as trace-reversed Ricci tensor. In Einstein Field Equation, it is used for describing spacetime curvature such that it is in alignment with the conservation of energy and momentum.  It is defined as:

G = R(-½) gR

Where, 

  • R is the Ricci tensor
  • g is the metric tensor
  • R is the scalar curvature

What is stress-energy tensor?

Stress-energy tensor is defined as the tensor Tαβ is a symmetrical tensor which is used for describing the energy and momentum density of the gravitational field. It is given as:

Tαβ = Tβα

Frequently Asked Questions – FAQs

Q1

Write the Einstein Field Equation?

The Einstein Field Equation is given by:
\(\begin{array}{l}G_{\mu \upsilon} + g_{\mu \upsilon} \Lambda = \frac{8\pi G}{c^4} T_{\mu \upsilon}\end{array} \)
Q2

What is the use of Einstein tensor in EFE?

In Einstein Field Equation, the Einstein tensor is used for describing spacetime curvature such that it is in alignment with the conservation of energy and momentum.
Q3

Write the expression for Einstein tensor?

The Einstein tensor is given by: G = R – (1/2)gR
Where,
  • R is the Ricci tensor
  • g is the metric tensor
  • R is the scalar curvature
Q4

What is stress-energy tensor?

Stress-energy tensor is defined as the tensor Tαβ is a symmetric tensor which is used for describing the energy and momentum density of the gravitational field.
Q5

What do you mean by EFE?

The Einstein Field Equation (EFE), also known as Einstein’s equation, is a set of ten nonlinear partial differential equations of the Einstein field extracted from Albert Einstein’s General Theory of Relativity . The EFE describes the basic interaction of gravitation.

Stay tuned with BYJU’S for more such interesting articles. Also, register to “BYJU’S – The Learning App” for loads of interactive, engaging Physics-related videos and an unlimited academic assistance.

Test Your Knowledge On Einstein Field Equation!
Quiz Image

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz

Congrats!

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

0 out of 0 arewrong
0 out of 0 are correct
0 out of 0 are Unattempted
PHYSICS Related Links
Cgs Unit Of Force Parts Of Dc Generator
Electrical Components With Names Momentum Example
Si Unit Of Potential Difference Electrical Energy
Gravitational Potential Energy Equation Ocean Thermal Energy Conversion
3 Laws Of Motion Dipole Moment Formula

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*

  1.  Aanshumaan Shrijai
    August 4, 2020 at 1:06 pm

    This was very helpful, thank you so much.

    Reply