From our previous studies, we are aware that Lenz’s law is consistent with the law of conservation of energy. Apart from the qualitative analysis, as done previously, the same can be proved quantitatively as well. Let us consider an example to prove this fact clearly.
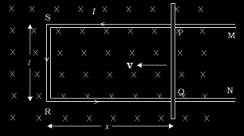
Rectangular loop to explain energy conservation
Let us consider a rectangular loop as shown in the figure above, with the sides PQ, QR, RS and SP. Here, the three sides of the loop are fixed and one of the sides, the side PQ, is free to move. Let r be the resistance of the movable arm under consideration. Also, let the resistance of the remaining arms QR, RS and SP be very small and negligible as compared to r. The overall resistance of the rectangular loop can be said to be r and we can also say that the resistance of the loop does not change with the motion in the loop. If the voltage applied across the loop be taken as ε, then the current in the loop can be given as,
As the coil is placed in the presence of a magnetic field and there is a current in the coil, a force acts on the arm PQ. We see that a force I (l × B) acts on the coil and is directed outwards, that is, in the direction opposite to the direction of the motion of the rod. The magnitude of the force acting on the arm can be given as,
Here, I is the current passing through the coil, l is the length of the arm, v is the velocity with which the arm moves in the field and B is the magnitude of the magnetic field acting on the system. Here, we note that the force acting on the arm arises due to the drift velocity of the charges in the rod, as the drift velocity is the entity that is responsible for the current in the rod. If the arm PQ is pushed with a constant velocity given by the magnitude v, we require a power to accomplish this push,
The energy that goes into the motion of the rod in this system is dissipated in the form of heat given by,
Here we see that the value of PJ is equal to the value of P.
Thus, mechanical energy which was needed to move the arm PQ is converted into electrical energy (the induced emf) and then to thermal energy. There is an interesting relationship between the charge flow through the circuit and the change in the magnetic flux. From Faraday’s law, we have learnt that the magnitude of the induced emf is,
However, as we know that,
And thus, from the above two equations, we can write,
To learn more about energy considerations and other related topics, download BYJU’S – The Learning App.



Comments