What is a Reynolds Number?
Reynolds number is a dimensionless quantity that is used to determine the type of flow pattern as laminar or turbulent while flowing through a pipe. Reynolds number is defined by the ratio of inertial forces to that of viscous forces.
Reynolds Number Formula
It is given by the following relation:
\(\begin{array}{l}R_{e}=\frac{\rho VD}{\mu }\end{array} \) |
Where,
- Re is the Reynolds number
- ρ is the density of the fluid
- V is the velocity of flow
- D is the pipe diameter
- μ is the viscosity of the fluid
If the Reynolds number calculated is high (greater than 2000), then the flow through the pipe is said to be turbulent. If Reynolds number is low (less than 2000), the flow is said to be laminar. Numerically, these are acceptable values, although in general the laminar and turbulent flows are classified according to a range. Laminar flow falls below Reynolds number of 1100 and turbulent falls in a range greater than 2200.
Laminar flow is the type of flow in which the fluid travels smoothly in regular paths. Conversely, turbulent flow isn’t smooth and follows an irregular math with lots of mixing.
An illustration depicting laminar and turbulent flow is given below.
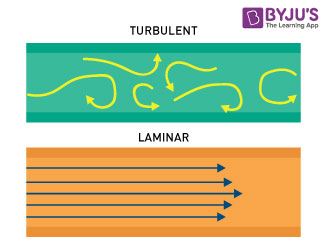
The Reynolds number is named after the British physicist Osborne Reynolds. He discovered this while observing different fluid flow characteristics like flow a liquid through a pipe and motion of an airplane wing through the air. He also observed that the type of flow can transition from laminar to turbulent quite suddenly.
Reynolds Number Example Problems
Problem 1- Calculate Reynolds number, if a fluid having viscosity of 0.4 Ns/m2 and relative density of 900 Kg/m3 through a pipe of 20 mm with a velocity of 2.5 m.
Solution 1 – Given that,
Viscosity of fluid μ
Density of fluid ρ
Diameter of the fluid
From the above answer, we observe that the Reynolds number value is less than 2000. Therefore, the flow of liquid is laminar.
Watch the video and understand the equation of continuity.

For more concepts in Physics, check out our YouTube Channel with loads of video modules to help you out only at BYJU’S.


this was really helpful