The lens is a transparent material which is bound by two surfaces. It has a principal axis, principal focus, centre of curvature of lens, aperture and optical centre.There are two types of lenses, they are a convex lens and a concave lens. The images obtained from these lenses can be either a real image or a virtual image. Below is an experiment to find the image distance for varying object distances of a convex lens with ray diagrams.
| Table of Contents |
Aim
To find the image distance for varying object distances in case of a convex lens and drawing corresponding ray diagrams to show the nature of the image formed.
Theory
What is a convex lens?
A convex lens is defined as a lens which is thick at the centre and thin at the edges. A convex lens is also known as a converging lens as it converges the light beam incident on it. There are three types of convex lens:
- Double convex lens
- Plano-convex lens
- Concavo-convex lens
What is lens formula?
Lens formula is defined as the relationship between object distance (u), image-distance (v) and the focal length (f). Following is the mathematical representation of lens formula:
\(\begin{array}{l}\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\end{array} \) |
Where,
- f is the focal length of the lens
- v is the distance of the image from the optical centre of the lens
- u is the distance of an object from the optical centre of the lens
Read More: Lens Formula
Materials Required
Following are the materials required for the experiment:
- A convex lens with a focal length of 12-20 cm.
- Measuring scale
- Optical bench
- A needle
- A candle
Experimental Setup

Procedure
- Place the convex lens on a lens holder, placing the screen on the other side of the lens.
- Try focusing the image to get a sharp, clear and inverted image on the screen. The focal length that is obtained is a rough focal length which can be measured using a meter scale.
- The position at which the lens is fixed, mark it as O.
- Once the focal length is calculated, mark point F on both the sides of the lens.
- Mark a point 2F, as the distance between the lens is double the focal length of the lens.
- Place the candle at a distance beyond 2F and adjust the height of the centre of the lens with the height of the flame.
- To obtain a sharp image of the candle flame in the convex lens, adjust the position of the screen and record the observations.
- Record the observations by placing the needle or lighted candle at 2F.
- Record the observations by shifting the object between F and 2F.
- Record the observations by placing the object at F.
- Record the observations by placing the object between O and F.
- Draw the ray diagrams for all the positions of the object.
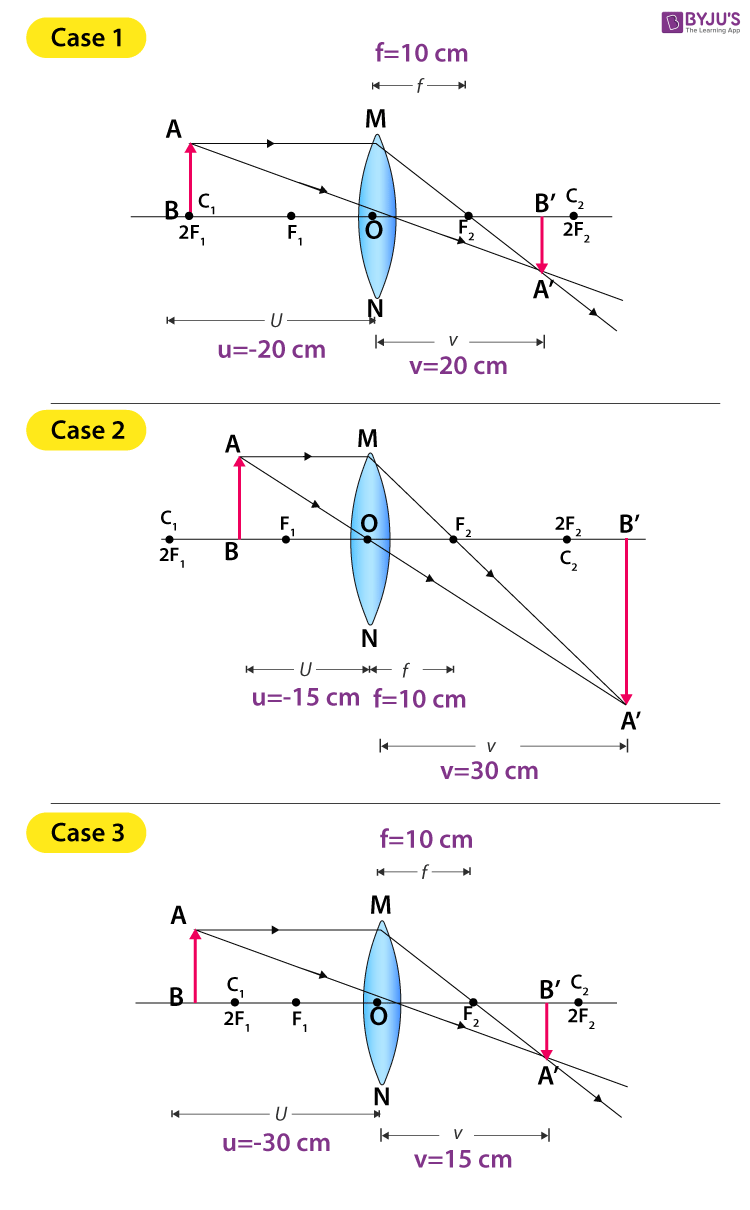
Ray Diagrams
Observation Table
| Sl. no | Postion of the optical centre O of the lens l (cm) | Position of candle a (cm) | Position of screen s (cm) | Distance between lens and candle (object distance) u=a-l (cm) | Distance between lens and screen (image distance) v=s-l (cm) | Focal length (l) |
| 1 | 50 | 30 | 70 | -20 | 20 | 10 cm |
| 2 | 50 | 35 | 80 | -15 | 30 | 10 cm |
| 3 | 50 | 20 | 65 | -30 | 15 | 10 cm |
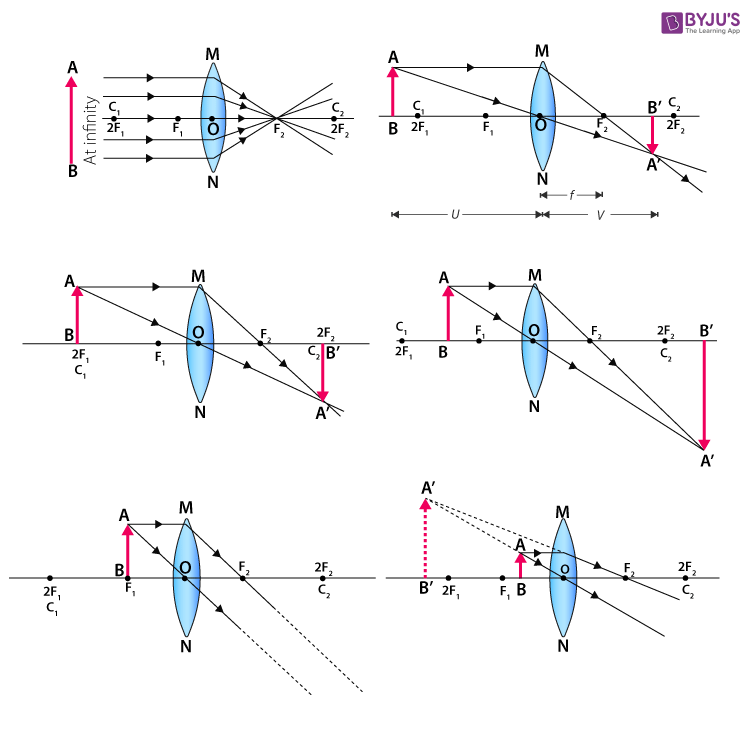
| 4 | 50 | 40 | No image obtained on screen | -10 | Infinity | |
| 5 | 50 | 45 | No image obtained on screen | -5 | Virtual image obtained and cannot be taken on screen |
Read More: Convex Lens
Calculations
Following is the calculations of f for different cases explaining the focal length of the given lens is 10cm:
| Case 1: \(\begin{array}{l}\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\Rightarrow \frac{1}{f}=\frac{1}{20}-(\frac{1}{-20})=\frac{2}{20}=\frac{1}{10}\Rightarrow f=10\;cm\end{array} \) |
| Case 2: \(\begin{array}{l}\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\Rightarrow \frac{1}{f}=\frac{1}{30}-(\frac{1}{-15})=\frac{3}{30}=\frac{1}{10}\Rightarrow f=10\;cm\end{array} \) |
| Case 3: \(\begin{array}{l}\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\Rightarrow \frac{1}{f}=\frac{1}{15}-(\frac{1}{-30})=\frac{3}{30}=\frac{1}{10}\Rightarrow f=10\;cm\end{array} \) |
Result
| S.no | Position of the object | Position of the image | Relative size of the image | Nature of the image |
| 1 | At 2F1 | At 2F2 | Same size | Real and inverted |
| 2 | Between F1 and 2F1 | Beyond 2F2 | Enlarged | Real and inverted |
| 3 | Beyond 2F1 | Between F2 and 2F2 | Diminished | Real and inverted |
| 4 | At focus F1 | At infinity | Infinitely large or highly enlarged | Real and inverted |
| 5 | Between focus F1 and optical center O | On the same side of the lens as the object | Enlarged | Virtual and erect |
| 6 | At infinity | At focus F2 | Highly diminished, point-sized | Real and inverted |
The focal length of the given lens is 10cm.
Precautions
- The convex lens must have the focal length between 15 to 20 cm.
- The convex lens must have a small aperture.
- To avoid the flickering of the candle flame, the experiment can be conducted in calm air.
- Perform the experiment in a dark room so as to obtain a distinct and sharp image of the candle flame.
- Image screen shouldn’t be shaky.
Viva Questions
Q1. What is a lens?
Ans: Lens is defined as a transparent material with curved sides on both the sides or one curved and one plane surface.
Q2. Define power of a lens.
Ans: Power of a lens is defined as the reciprocal of the focal length. The mathematical formula is given as:
\(\begin{array}{l}P=\frac{1}{f}\end{array} \) |
Where,
- P is the power of a lens
- f is the focal length
Q3. What is one dioptre?
Ans: One dioptre is defined as a unit of measurement of the optical power of a curved mirror or a lens. It is given as follows:
| 1 dioptre = 1m-1 |
Q4. What is meant by principal of axis?
Ans: Principle of axis is defined as the line passing through the centre of the lens or a spherical mirror.
Q5. What is the focal length of a lens?
Ans: Focal length of a lens is defined as the distance between the principal focus and the optical centre.
|
Related Articles: |
Stay tuned with BYJU’S to learn more about other Physics-related experiments.


Comments