Scientists use many skills to investigate the world around them. They make observations and gather information from their senses. Some observations are as simple as figuring out the texture and colour of an object. However, scientists may need to take measurements if they want to know more about a substance. Measurement is one of the important aspects of science. It is difficult to conduct experiments and form theories without the ability to measure. Thus, to measure unknown resistance in a circuit, Samuel Hunter Christie invented the Wheatstone bridge in 1833, which Sir Charles Wheatstone later popularised in 1843.
What is Wheatstone Bridge?
Wheatstone bridge, also known as the resistance bridge, calculates the unknown resistance by balancing two legs of the bridge circuit. One leg includes the component of unknown resistance.
The Wheatstone Bridge Circuit comprises two known resistors, one unknown resistor and one variable resistor connected in the form of a bridge. This bridge is very reliable as it gives accurate measurements.
Construction of Wheatstone Bridge
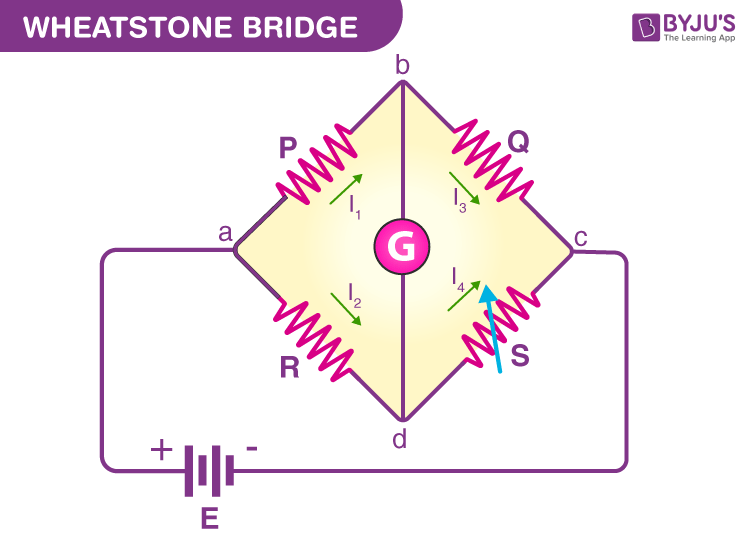
A Wheatstone bridge circuit consists of four arms, of which two arms consist of known resistances while the other two arms consist of an unknown resistance and a variable resistance. The circuit also consists of a galvanometer and an electromotive force source. The emf source is attached between points a and b while the galvanometer is connected between points c and d. The current that flows through the galvanometer depends on its potential difference.
What is the Wheatstone Bridge Principle?
The Wheatstone bridge works on the principle of null deflection, i.e. the ratio of their resistances is equal, and no current flows through the circuit. Under normal conditions, the bridge is in an unbalanced condition where current flows through the galvanometer. The bridge is said to be balanced when no current flows through the galvanometer. This condition can be achieved by adjusting the known resistance and variable resistance.
Wheatstone Bridge Derivation
The current enters the galvanometer and divides into two equal magnitude currents as I1 and I2. The following condition exists when the current through a galvanometer is zero,
The currents in the bridge, in a balanced condition, are expressed as follows:
Here, E is the emf of the battery.
By substituting the value of I1 and I2 in equation (1), we get
Equation (2) shows the balanced condition of the bridge, while (3) determines the value of the unknown resistance.
In the figure, R is the unknown resistance, S is the standard arm of the bridge and P and Q are the ratio arm of the bridge.
Wheatstone Bridge Formula
Following is the formula used for the Wheatstone bridge:
\(\begin{array}{l}R=\frac{PS}{Q}\end{array} \) |
Where,
- R is the unknown resistance
- S is the standard arm of the bridge
- P and Q is the ratio of the arm of the bridge
| Related Articles: |
Wheatstone Bridge Application
- The Wheatstone bridge is used for the precise measurement of low resistance.
- Wheatstone bridge and an operational amplifier are used to measure physical parameters such as temperature, light, and strain.
- Quantities such as impedance, inductance, and capacitance can be measured using variations on the Wheatstone bridge.
Wheatstone Bridge Limitations
- For low resistance measurement, the resistance of the leads and contacts becomes significant and introduces an error.
- For high resistance measurement, the measurement presented by the bridge is so large that the galvanometer is insensitive to imbalance.
- The other drawback is the resistance change due to the current’s heating effect through the resistance. Excessive current may even cause a permanent change in the value of resistance.
Frequently Asked Questions – FAQs
What is Wheatstone Bridge?
What is the Wheatstone Bridge Principle?
When is the Wheatstone Bridge balanced?
When is the Wheatstone Bridge said to be unbalanced?
What are the limitations of Wheatstone Bridge?
Watch the video and learn to solve numerical questions on Wheatstone Bridge.
s
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Thanks a lot . Very useful . I now understand what the Wheatstone bridge is all about .
Thanks for this . it is very helpfull to me.
Very nice and easy for studying.
Thank you it was excellent
thank you
nicely explained.
Nice explanation
Nice Byju’s the learning aap for helping us in due to covid-19 situation
Good☺