Biot-Savart Law

We know that electromagnetism is an important branch of Physics that deals with electromagnetic force. It typically deals with magnetic force and electric current. Let us know about the law that relates magnetic fields to the electric current – Biot-Savart Law.

Table of Contents

What isΒ Biot-Savart Law?

Biot-Savart’s law is an equation that gives the magnetic field produced due to a current carrying segment. This segment is taken as a vector quantity known as the current element.

Biot Savart Law

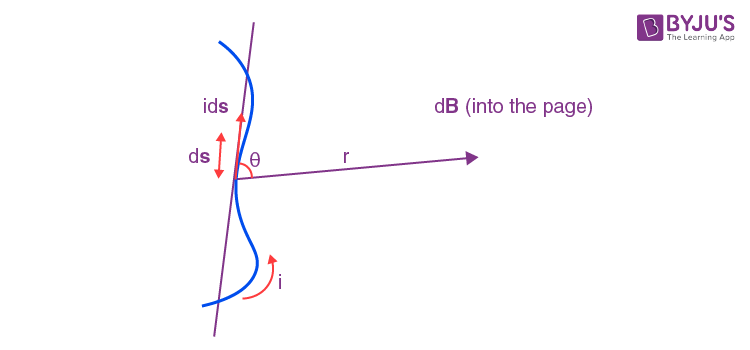
What is the Formula ofΒ Biot-Savart’s Law?

Consider a current carrying wire β€˜i’ in a specific direction as shown in the above figure. Take a small element of the wire of length ds. The direction of this element is along that of the current so that it forms a vector ids.

To know the magnetic field produced at a point due to this small element, one can apply Biot-Savart’s Law. Let the position vector of the point in question drawn from the current element be r and the angle between the two be ΞΈ. Then,

\(\begin{array}{l}\left| dB\right|=(\frac{\mu _0}{4\pi })(\frac{Ids\,sin\theta }{r^2})\end{array} \)

Where, ΞΌ0 is the permeability of free space and is equal to 4Ο€ Γ— 10-7 TmA-1.

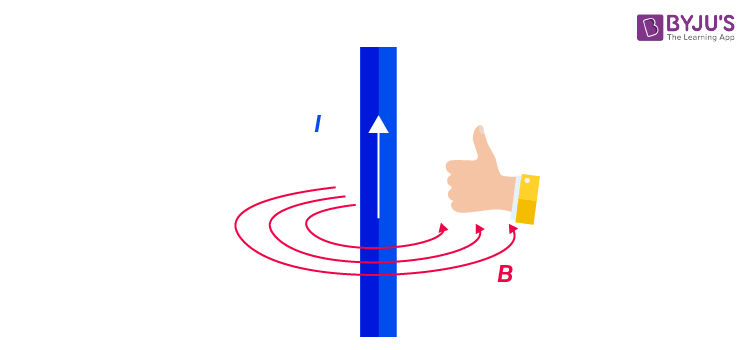
The direction of the magnetic field is always in a plane perpendicular to the line of element and position vector. It is given by the right-hand thumb rule where the thumb points to the direction of conventional current and the other fingers show the magnetic field’s direction.

Biot Savart Law
In the figure shown above, the direction of the magnetic field is pointing into the page.

Applications ofΒ Biot-Savart’s Law

Some ofΒ Biot-Savart’s Law applications are given below.

  • We can use Biot–Savart law to calculate magnetic responses even at the atomic or molecular level.
  • It is also used in aerodynamic theory to calculate the velocity induced by vortex lines.

Importance of Biot-Savart Law

Following are the importance of the Biot-Savart law:

  • Biot-Savart law is similar to Coulomb’s law in electrostatics.
  • The law is applicable for very small conductors too which carry current.
  • The law is applicable for symmetrical current distribution.

Accelerate Your JEE Main & Advanced Exam Preparation by
Watching this Video about Magnetism and Force on Dielectric in Charged Capacitor

Solved Problems on Biot-Savart Law

Q1. Determine the magnitude of the magnetic field of a wire loop at the centre of the circle with radiusΒ RΒ and currentΒ I.

Ans:Β The magnitude of the magnetic field of the wire loop is given as:

\(\begin{array}{l}\frac{\mu _{0}I}{2R}\end{array} \)

Q2. A circular coil of radius 5Β Γ— 10-2Β m and with 40 turns is carrying a current of 0.25 A. Determine the magnetic field of the circular coil at the centre.

Ans:Β The radius of the circular coil =Β 5Β Γ— 10-2Β m

Number of turns of the circular coil = 40

Current carried by the circular coil = 0.25 A

Magnetic field is given as:Β 

\(\begin{array}{l}B=\frac{\mu _{0}NI}{2a}\end{array} \)

=Β 

\(\begin{array}{l}\frac{4\pi \times 10^{-7}T.m/A(40)0.25A}{2.50\times 10^{-2}m}\end{array} \)

= 1.2Β Γ— 10-4Β T

Q3. Determine the magnetic field at the centre of the semicircular piece of wire with a radius 0.20 m. The current carried by the semicircular piece of wire is 150 A.

Ans:Β The radius of the semicircular piece of wire = 0.20 m

Current carried by the semicircular piece of wire = 150 A

Magnetic field is given as:Β 

\(\begin{array}{l}B=\frac{\mu _{0}NI}{2a}\end{array} \)

The differential form of Biot-Savart law is given as:Β 

\(\begin{array}{l}dB=\frac{\mu _{0}I}{4\pi }\frac{dIsin\theta }{r^{2}}\end{array} \)
\(\begin{array}{l}B=\frac{\mu _{0}}{4\pi }I\int \frac{dI\times \hat{r}}{r^{2}}\end{array} \)
\(\begin{array}{l}=\frac{\mu _{0}}{4\pi }\frac{I}{r^{2}}\int dI\end{array} \)
\(\begin{array}{l}=\frac{\mu _{0}}{4\pi }\frac{I}{r^{2}}\pi r\end{array} \)
\(\begin{array}{l}=\frac{\mu _{0}I}{4r}\end{array} \)
\(\begin{array}{l}=\frac{4\pi \times 10^{-7}T.m/A(150A)}{4(0.20m)}\end{array} \)

=2.4Γ—10-4 T

Moving Charges and Magnetism Lecture in Hindi



Frequently Asked Questions – FAQs

Q1

Which law of electricity is Biot Savart law of magnetism analogous to?

Biot-Savart law in magnetism is analogous to Coulomb’s law in electricity. According to Biot Savart law, magnetic flux density

\(\begin{array}{l}H=\frac{\mu _{0}I.dl\;sin\theta }{4\pi r^{2}}\end{array} \)
which is analogous to the electric field
\(\begin{array}{l}F=\frac{q_{1}q_{2}}{4\pi\epsilon _{0} r^{2}}\end{array} \)
which is Coulomb’s law.

Q2

Name one property that cannot be calculated using the Biot Savart law.

Electric field intensity cannot be calculated using the Biot Savart law. It is used for calculating the magnetic field intensity. This is further used for calculating the flux density and permeability using the formula

\(\begin{array}{l}B=\mu H\end{array} \)
.

Q3

Consider a circular conductor with 2m radius and 8A current flowing through it. Determine the magnetic field intensity at the centre of the circular conductor.

By using the formula

\(\begin{array}{l}B=\frac{\mu _{0}I}{2R}\end{array} \)
we can determine the magnetic field intensity.
Substituting the values for current I = 8A and radius R = 2m, we get B =
\(\begin{array}{l}8\pi \times 10^{-7}T\end{array} \)
.

Q4

What is the magnetic field at the centre of the conductor when the conductor is subjected to a current of 9A and with infinite radius?

The formula used for calculating the magnetic field is

\(\begin{array}{l}\frac{\mu _{0}I}{2R}\end{array} \)
Since R is infinite, the magnetic field will be 0.

Q5

Can electric field intensity be computed using Biot Savart’s Law?

No, electric field intensity cannot be computed using Biot Savart’s law.

Video Lecture About the Basic Concepts of Biot Savart

Test your knowledge on Biot Savart law
Quiz Image

Put your understanding of this concept to test by answering a few MCQs. Click β€˜Start Quiz’ to begin!

Select the correct answer and click on the β€œFinish” button
Check your score and answers at the end of the quiz

Congrats!

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

0 out of 0 arewrong
0 out of 0 are correct
0 out of 0 are Unattempted
PHYSICS Related Links
Speed Definition Science Forced Oscillation
Scalar Product Forced Vibration Definition
Charge Definition Physics Gamma Rays Wavelength
Internal Reflection Uses Of Ac Generator
10 Uses Of Concave Mirror Laws Of Static Friction