Doppler Effect

Doppler Effect Examples

Let us imagine the following scenario:

Case 1: Two people A and B, are standing on the road, as shown below in the picture.

Which person hears the sound of the revving engine with a greater magnitude?

Person A hears the sound of the revving engine with a greater magnitude than person B. Person B, standing behind the car, receives fewer waves per second (because they’re spread out), resulting in a low-pitched sound. But, person A who is in front of the car, receives more of those soundwave ripples per second. As a result, the frequency of the waves is higher, which means the sound has a higher pitch.

Case 2: Now let us consider the following situations:

Situation 1: How is the pattern of waves formed when you suddenly jump into a pond?
Situation 2: How is the pattern of waves formed when you are walking in a pond?

The image given below highlights the difference between wave patterns in both situations.

The difference in the wave pattern is due to the source’s movement in the second case. This is what the Doppler effect is. In the Doppler effect, the frequency received by the observer is higher during the approach, identical when the relative positions are the same, and keeps lowering on the recession of the source.

In this video let’s see how relative motion between the source and the observer changes the frequency of sound waves giving rise to the Doppler Effect.

Doppler Effect Formula

Doppler effect is the apparent change in the frequency of waves due to the relative motion between the source of the sound and the observer. We can deduce the apparent frequency in the Doppler effect using the following equation:

While there is only one Doppler effect equation, the above equation changes in different situations depending on the velocities of the observer or the source of the sound. Let us see below how we can use the equation of the Doppler effect in different situations.

(a) Source Moving Towards the Observer at Rest

In this case, the observer’s velocity is zero, so V₀ is equal to zero. Substituting this into the Doppler effect equation above, we get the equation of the Doppler effect when a source is moving towards an observer at rest as:

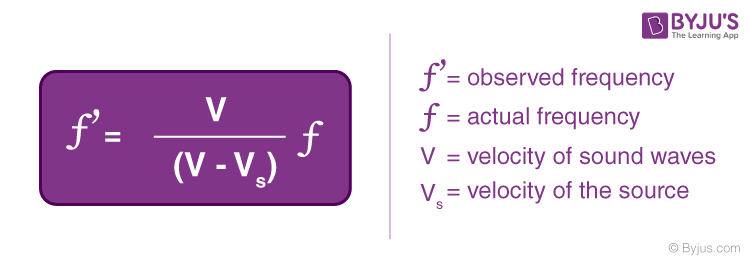
(b) Source Moving Away from the Observer at Rest

Since the velocity of the observer is zero, we can eliminate V₀ from the equation. But this time, the source moves away from the observer, so its velocity is negative to indicate the direction. Hence, the equation now becomes as follows:

(c) Observer Moving Towards a Stationary Source

In this case, v_s will equal to zero, hence we get the following equation:

(d)Observer Moving Away from a Stationary Source

Since the observer is moving away, the velocity of the observer becomes negative. So, instead of adding V₀, we now subtract, since V₀ is negative.

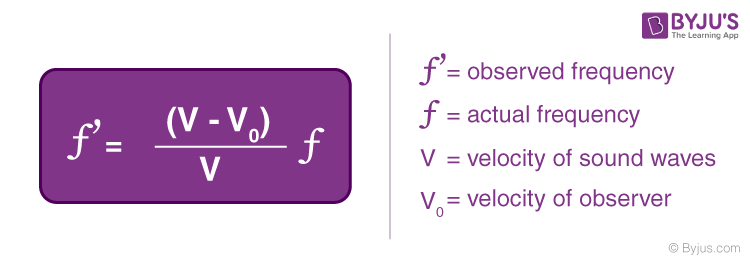
Doppler Effect Solved Problems

Two trains A and B are moving toward each other at a speed of 432 km/h. If the frequency of the whistle emitted by A is 800 Hz, then what is the apparent frequency of the whistle heard by the passenger sitting in train B. (The velocity of sound in air is 360 m/s).

Solution:

The source and the observer are moving toward each other, hence.

\(\begin{array}{l}f=f_0(\frac{v+v_{o}}{v-v_{s}})\end{array} \)

Converting 432 km/h into m/s we get 120 m/s.

Substituting the values in the equation, we get

\(\begin{array}{l}f=800(\frac{360+120}{360-120})=1600\,Hz\end{array} \)

Apparent frequency f = 1600 Hz

2. A bike rider approaching a vertical wall observes that the frequency of his bike horn changes from 440 Hz to 480 Hz when it gets reflected from the wall. Find the speed of the bike if the speed of sound is 330 m/s.

Solution:

Let the bike approach the wall with speed u.

Then the apparent frequency received by the wall can be calculated as

\(\begin{array}{l}f=f_0(\frac{v}{v-u})… (1)\end{array} \)

For the reflected wave,

\(\begin{array}{l}f’=f(\frac{v+u}{v})… (2)\end{array} \)

Substituting (1) in (2), we get

\(\begin{array}{l}f’=f_0(\frac{v}{v-u})\times (\frac{v+u}{v})\end{array} \)

Simplifying, we get

\(\begin{array}{l}f’=(\frac{v+u}{v-u})f_0\end{array} \)

Substituting the values in the equation, we get

\(\begin{array}{l}480=(\frac{v+u}{v-u})440\end{array} \)

\(\begin{array}{l}\frac{480}{440}=(\frac{v+u}{v-u})\end{array} \)

\(\begin{array}{l}u=\frac{4}{92}\times 330=14.3\,m/s\end{array} \)

The speed of the bike is 14.3 m/s

Let us see more solved examples in the video given below

Uses of Doppler Effect

Many people mistake the Doppler effect to be applicable only for sound waves. It works with all types of waves including light. Below, we have listed a few applications of the doppler effect:

• Sirens
• Radar
• Astronomy
• Medical Imaging
• Blood Flow Measurement
• Satellite Communication
• Vibration Measurement
• Developmental Biology
• Audio
• Velocity Profile Measurement

Doppler Effect Limitations

• Doppler Effect is applicable only when the velocities of the source of the sound and the observer are much less than the velocity of sound.
• The motion of both source and the observer should be along the same straight line.

Doppler Effect In Light

Doppler effect of light can be described as the apparent change in the frequency of the light observed by the observer due to relative motion between the source of light and the observer.
For sound waves, however, the equations for the Doppler shift differ markedly depending on whether it is the source, the observer, or the air, which is moving. Light requires no medium, and the Doppler shift for light travelling in a vacuum depends only on the relative speed of the observer and source.

Red Shift and Blue Shift

• When the light source moves away from the observer, the frequency received by the observer will be less than the frequency transmitted by the source. This causes a shift towards the red end of the visible light spectrum. Astronomers call it the redshift.
• When the light source moves towards the observer, the frequency received by the observer will be greater than the frequency transmitted by the source. This causes a shift towards the high-frequency end of the visible light spectrum. Astronomers call it the blue shift.

The below video provides an in-depth analysis of Doppler Effect for JEE Advanced 2023

Frequently Asked Questions – FAQs

Q1

What is the Doppler Effect in Physics?

Doppler Effect in physics refers to the change in wave frequency during the relative motion between a wave source and its observer.

Q2

Who discovered the Doppler Effect?

Christian Johann Doppler, an Austrian mathematician and physicist discovered the Doppler effect in 1842.

Q3

Can Doppler effect be observed in both longitudinal and transverse waves?

Yes, Doppler effects can be observed for both types of waves. Doppler effect in sound (longitudinal waves) and the Doppler effect in light (transverse waves) are well-known phenomena.

Q4

How can the Doppler Effect be applied to everyday life?

A few daily life examples of the Doppler effect are: a) When you stand beside a police radar. b) The Doppler effect is used by meteorologists to track storms. c) Doctors use the Doppler Effect in hospitals to diagnose heart problems. d) Traffic police make use of the doppler effect a radar gun to check the speed of the oncoming vehicles.

Why is the Doppler Effect used in hospitals?

Q5

Why is the Doppler Effect used in hospitals?

Doppler effect in hospitals is used to monitor blood flow. Blood clots are also detected with the Doppler effect.

Q6

How does the Doppler Effect prove that the universe is expanding?

The Doppler effect is evidence that the universe is expanding. Edwin Hubble used the Doppler effect to prove that the universe is expanding. Hubble noticed that the light from distant galaxies was shifted toward lower frequencies to the red end of the spectrum. When stars or galaxies are moving away from us, we see their colour as red-shifted.

Stay tuned to BYJU’S and Fall in Love with Learning!