At a given point, the potential due to a dipole is

the sum of potentials due to each charge of dipole

the ratio of potentials due to each charge of dipole

the difference of potentials due to each charge of dipole

the product of potentials due to each charge of dipole

The direction of dipole moment is from

both the charges to the centre of dipole

Electric Potential Of A Dipole and System Of Charges

Before we understand the characteristics of the electric potential of a dipole, let us quickly review our understanding of dipole and electric potential. An electric potential is the amount of work needed to move a unit positive charge from a reference point to a specific point inside an electric field without producing acceleration. A dipole is a pair of opposite charges with equal magnitudes separated by a distance, d.

The electric potential due to a point charge q at a distance of r from that charge is given by,

\(\begin{array}{l}V = \frac{1}{4πε_0}~\frac{q}{r}\end{array} \)

Where ε₀ is the permittivity of free space.

The electric potential is a scalar field whose gradient becomes the electrostatic vector field. Since it is a scalar field, it is easy to find the potential due to a system of charges. It is the summation of the electric potentials at a point due to individual charges.

Thus, we can write the net electric potential due to the individual potentials contributed by charges as

\(\begin{array}{l}V_{net} = \sum\limits_{i}~V_{i}\end{array} \)

\(\begin{array}{l}V_{net} = \frac{1}{4πε_0}~\sum\limits_{i}~\frac{q_i}{r_i}\end{array} \)

Let us use this concept to find the electric field of a dipole. Let the distance between the point P and the positive and negative charges be r₊ and r_– respectively. Let the distance from the midpoint of the dipole be r. Let this vector subtend an angle θ to the dipole axis. Thus using the above theorem, we have,

\(\begin{array}{l}V = \sum_{i}~V_i = V_{+}~+~V_{-}\end{array} \)

\(\begin{array}{l}V = \frac{1}{4πε_0}~\left(\frac{q}{r_{+}}~ +~\frac{-q}{r_{-}}\right)\end{array} \)

\(\begin{array}{l}V = \frac{q}{4πε_0}\left(\frac{1}{r_{+}}~ -~\frac{1}{r_{-}} \right)\end{array} \)

\(\begin{array}{l}V = \frac{q}{4πε_0}~\left(\frac{r_{-}~-~r_{+}}{r_{+}~ r_{-}}\right)\end{array} \)

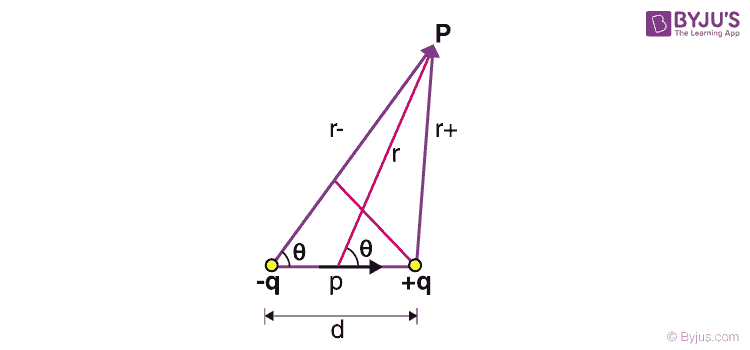
If the point P is sufficiently far from the dipole, then we can approximate

\(\begin{array}{l}r_{-} ≈ r_{+} ≈ r\end{array} \)

And by drawing a line perpendicular to r_– from +q we can write,

\(\begin{array}{l}r_{-}~-~r_{+} ≈ d cos~θ\end{array} \)

Thus, we can write the potential as:

\(\begin{array}{l}V = \frac{q}{4πε_0}~\left(\frac{d ~cos~θ}{r^2}\right)\end{array} \)

We know that the magnitude of the electric dipole moment is:

\(\begin{array}{l}|\overrightarrow{p}| = p = q~.~d\end{array} \)

Thus, electric potential due to a dipole at a point far away from the dipole is given by,

\(\begin{array}{l}V = \frac{1}{4πε_0}~ \frac{p~ cos~θ}{r^2}\end{array} \)

Notice that the potential falls off by r² while the electric field falls off by r³. Also, note that when the angle is 90⁰, the point P is equidistant to both charges, and the electric potential is zero. When θ > 90⁰, the potential is negative because the point P is closer to the negative charge.

Important JEE questions on Electrostatic Potential and Capacitance

Know About Electric Field due to Dipole

Stay tuned with BYJU’S for more such interesting articles. Also, register to “BYJU’S – The Learning App” for loads of interactive, engaging Physics-related videos and an unlimited academic assist.

Frequently Asked Questions – FAQs

What is an electric charge?

Electric charge is the basic physical property of matter that causes it to experience a force when kept in an electric or magnetic field. An electric charge is associated with an electric field, and the moving electric charge generates a magnetic field. An electric charge can be negative or positive. Unlike charges attract and like charges repel each other.

What is electric potential?

Electric potential is the amount of work required to displace a unit charge from a reference point to the desired point against an electric field.

What is the SI unit of the dipole moment?

The SI unit of dipole moment is coulomb metre.

What is an electric dipole?

An electric dipole is defined as a couple of opposite charges q and –q separated by a distance d. The midpoint q and –q is called the centre of dipole.

What is the direction of an electric dipole moment?

The electric dipole moment is a vector quantity, and it has a well-defined direction which is from the negative charge to the positive charge.

PHYSICS Related Links
Science Inventions And Discoveries	Unit Of Magnetic Field
Difference Between Solstice And Equinox	Unit Of Distance
Unit Of Frequency	Helmholtz Free Energy
Unit Of Capacitance	Spintronics
Wavelength Unit	Unit Of Inductance

PHYSICS Related Links

Science Inventions And Discoveries

Unit Of Magnetic Field

Difference Between Solstice And Equinox

Unit Of Distance

Unit Of Frequency

Helmholtz Free Energy