Discovered by Willebrord Snell in 1621, the laws of refraction are also termed Snell’s law. As we know, the refraction or bending of light takes place when it travels from medium to medium. The degree of bend is predicted with the help of this law. To comprehensively understand a discussion on lenses and their application, one must be familiar with the concepts of refraction.
| Table of Contents |
Snell’s Law – The Laws of Refraction
The point of refraction is created where the incident rays lands and the angle that it makes with the refracted ray not forgetting the normal line that is dropped on the plane perpendicularly. The medium through which the rays of light are passing creates a considerable difference in refraction unlike in reflection of light. The refractive indices make the dependency on the medium apparent in Snell’s Law.
The following is a diagrammatic representation:
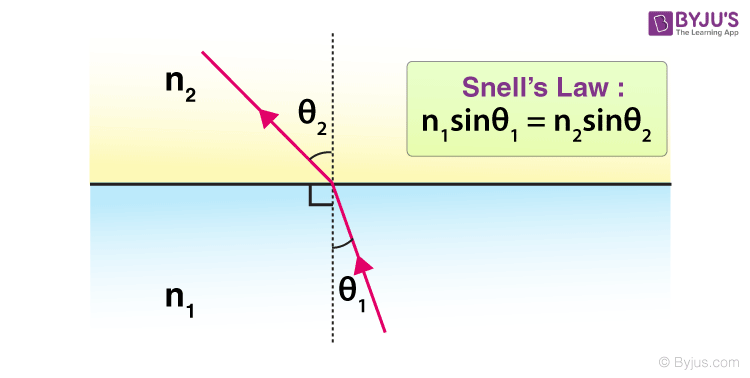
- n1 and n2 are the two different mediums that will impact the refraction.
- The refractive index of water is 1.33 whereas the refractive index of air is 1.00029.
- Thus, to understand the concept of Snell’s Law let’s consider the light of wavelength 600 nm that goes from water into the air.
- To calculate the angle made by the outgoing ray we apply the figures in the formula mentioned above.
- 1.33 sin 30o = 1.00029 sin x
- x = 41o
The normal on the surface is used to gauge the angles that the refracted ray creates at the contact point.
When one fishes with a spear it is not as difficult as fishing with a rod, as the fisherman has to encounter refraction in the latter case.
Watch the video and learn more about the chapter the Human Eye and Colourful World Class 10
| Related Articles |
Complex Snell’s Law Diagram
A complex diagram of Snell’s Law displays something that is not directly obvious. A ray of light passes through the glass and standing behind it the viewer experiences refraction through three media. The situation is represented in the following diagram.
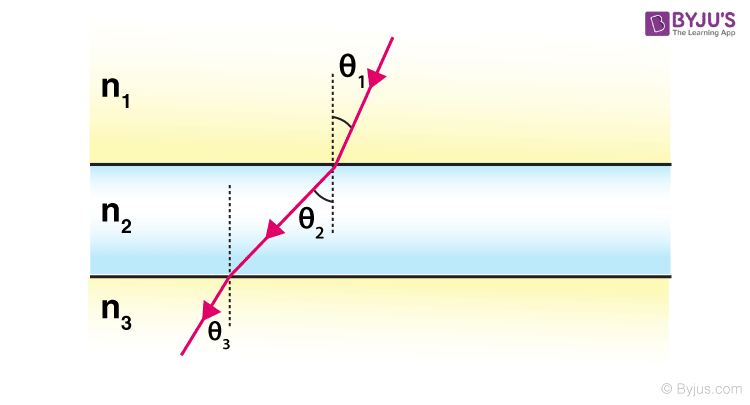
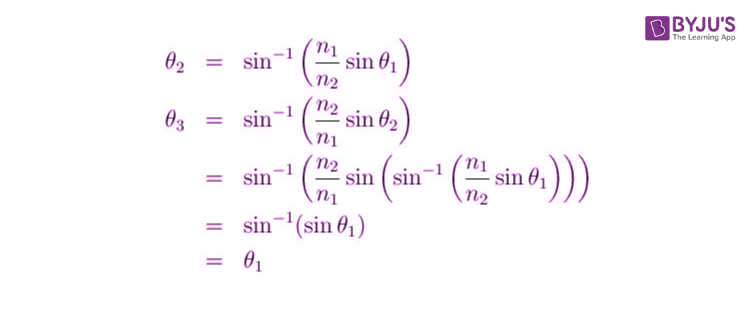
What we see in this is that the light ray incoming is parallel to the outgoing light ray.
As the angle of incidence (i) and angle of refraction (r) thus rearranging Snell’s Law:
- n1sin(i) = n2sin(r)
- (n1/n2)sin(i) = sin(r)
This gives us a qualitative representation of refraction. Thus, we’ll use this equation to understand the concept of multiple refractions. When moving from a section of the high index to a region of a low index, the ray will refract away from the normal. When the ray moves from a section of the lower index to the higher index the ray of incidence will bend towards the normal.
Watch the video to visualise the refraction of light through a glass prism
Frequently Asked Questions – FAQs
What is Snell’s law in physics?
Why is used of Snell’s law?
What is the angle of refraction?
What causes refraction?
What factors affect refraction?
- Temperature
- Wavelength
The below videos help to revise the chapter Light Reflection and Refraction Class 10
 |
 |
Stay tuned to BYJU’S and Fall in Love with Learning!
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments