Potential energy of a dipole in an external field

Potential energy of a dipole

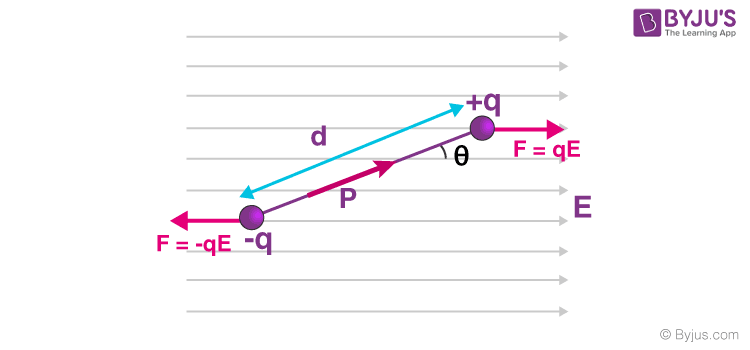
Consider a dipole with charges q₁ = +q and q₂ = -q placed in a uniform electric field as shown in the figure above. The charges are separated by a distance d and the magnitude of an electric field is E. The force experienced by the charges is given as –qE and +qE, as can be seen in the figure.

As we know that, when a dipole is placed in a uniform electric field, both the charges as a whole do not experience any force, but it experiences a torque equal to τ which can be given as,

This torque rotates the dipole unless it is placed parallel or anti-parallel to the field. If we apply an external and opposite torque, it neutralizes the effect of this torque given by τ_ext and it rotates the dipole from the angle Ɵ₀ to an angle Ɵ₁ at an infinitesimal angular speed without any angular acceleration.

The amount of work done by the external torque can be given by

As we know that the work done in bringing a system of charges from infinity to the given configuration is defined as the potential energy of the system, hence the potential energy U(Ɵ)  can be associated with the inclination Ɵ of the dipole using the above relation.

From the above equation, we can see that the potential energy of dipole placed in an external field is zero when the angle Ɵ is equal to 90° or when the dipole makes an angle of 90°.

Considering the initial angle to be the angle at which the potential energy is zero, the potential energy of the system can be given as,

To learn more about the potential energy of a dipole in an external electric field and other related topics, download BYJU’S – The Learning App.

What is Kinetic Energy and Potential Energy?