Have you ever thought about why we can see our image in a plane mirror? Itβs because of the phenomenon known as reflection. Light waves, sound waves, and water waves can undergo reflection. In this session, let us learn about the reflection of light and the types of reflection in detail.
| Table of Contents |
What Is Reflection of Light?
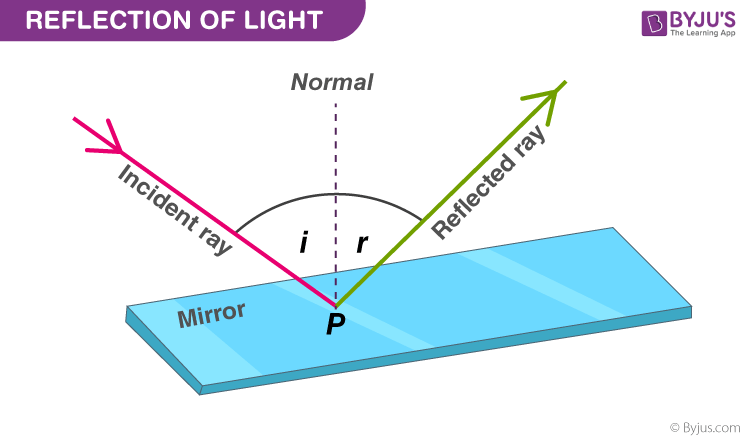
When a ray of light hits a polished surface, and the ray bounces back, it is known as the reflection of light. The incident light ray that falls on the surface is reflected off the polished surface. The light ray that bounces back is known as the reflected ray. A perpendicular drawn on a reflecting surface is called normal.
What Are the Laws of Reflection?
The laws of reflectionΒ are divided into two main points and they are:
- The angle of incidence is equal to the angle of reflection.
- The incident ray, reflected ray, and the normal at the point of incidence all lie in the same plane.
Watch the video and learn more about laws of reflection
Read More: Laws of Reflection
What Is Reflection on a Plane Mirror?
When the light rays get stroked on the flat mirror, they get reflected back. According to the laws of reflection, the angle of reflection is equal to the angle of incidence. The image is obtained behind the plane, which is present in the mirror. This process of obtaining a mirror image which is virtual and erect is known as a reflection on a plane mirror.
See the video below to learn about the reflection on a plane mirror
Characteristics of Image formed by Plane Mirror
Following are the characteristics of an image formed by the plane mirror:
- The image obtained by the plane mirror is always erect and virtual.
- The image size and the size of the object, both are equal.
- The distance between the image obtained and the mirror is the same as the distance at which the object is placed.
- Laterally inverted images are obtained.
Types of Reflection
Following are the two types of reflection of light:
- Specular or regular reflection
- Diffused or irregular reflection
Read More: Types of Reflection
Image Formed by the Plane Mirror
Consider the light rays 1, 2 and 3 shown by solid lines. The wavefronts which are perpendicular to these light rays are shown by the thin lines. The secondary wavefronts generated are the circular fronts described.
At point a, a wavefront is generated due to the secondary source on ray 2. At the same time, other wavefronts are generated at points c and b. Since wavefronts at points,Β a and b are generated at the same time ac = cb. Thus, the triangle acb is isosceles and the angles ΞΈ1 = ΞΈ2.
Note that ΞΈ1 is the angle of incidence and ΞΈ2 is the angle of reflection.
Thus,Β Angle of incidence = Angle of reflection
Below is theΒ image formed by the plane mirror
Related Article:
Watch the video and revise all the important concepts in the chapter Light Reflection and Refraction Class 10
Frequently Asked Questions β FAQs
What is meant by the reflection of light?
What is the nature of the image formed by the plane mirror?
State the laws of reflection.
- The angle of incidence is equal to the angle of reflection.
- The incident ray reflected ray and the normal at the point of incidence all lie in the same plane.
What are the types of reflection of light?
- Regular or specular reflection
- Irregular or diffused reflection
Which type of reflection results in a clear and sharp reflection?
Stay tuned to BYJUβS and Fall in Love with Learning!
Put your understanding of this concept to test by answering a few MCQs. Click βStart Quizβ to begin!
Select the correct answer and click on the βFinishβ button
Check your score and answers at the end of the quiz
Visit BYJUβS for all Physics related queries and study materials
Your result is as below
Comments