We learned about force in our previous sessions. Torque is the tendency of a force that tends to cause rotation. Let us learn about torque, SI unit of torque, types of torque, examples of torque, and how torque is calculated.
| Table of Contents: |
What Is Torque?
Torque is the measure of the force that can cause an object to rotate about an axis. Force is what causes an object to accelerate in linear kinematics. Similarly, torque is what causes an angular acceleration. Hence, torque can be defined as the rotational equivalent of linear force. The straight line about which the object rotates is called the axis of rotation. In physics, torque is simply the tendency of a force to turn or twist. Different terminologies such as moment or moment of force are interchangeably used to describe torque. The distance of the point of application of force from the axis of rotation is sometimes called the moment arm or lever arm.
Types of Torque
Torque can be either static or dynamic. Static torque is a torque that does not produce an angular acceleration. A few examples of static torque are as follows:
• A person pushing a closed-door is applying a static torque because the door isn’t rotating despite the force applied.
• Pedalling a cycle at a constant speed is also an example of static torque as there is no acceleration.
The drive shaft in a racing car accelerating from the start line exhibits dynamic torque because it must be producing an angular acceleration of the wheels, given that the car is accelerating along the track.
To explain torque in detail let us consider the figure.
- We can see that the net force on the body is zero if the magnitude of forces F1 and F2 are equal.
- Hence, the body is in translational equilibrium.
- But it tends to rotate, thus the turning effect produced by force is known as moment of force or torque.
Now we will consider the example of a door and try to formulate the equation for torque.
- If we apply force closer to the hinge, then a larger force is required to rotate the door.
- Also, it depends on the direction in which the force is being applied.
- If it is perpendicular to the line joining the hinge and the point of application of force then a smaller force is required.
How Is Torque Calculated?
A simple way to calculate the magnitude of the torque is to first determine the lever arm and then multiply it times the applied force.
Now, from the above observation, we conclude that the torque produced depends on the magnitude of the force and the perpendicular distance between the point about which torque is calculated and the point of application of force. So, mathematically torque is represented as:
where r is the length of the lever arm and θ is the angle between the force vector and the lever arm.
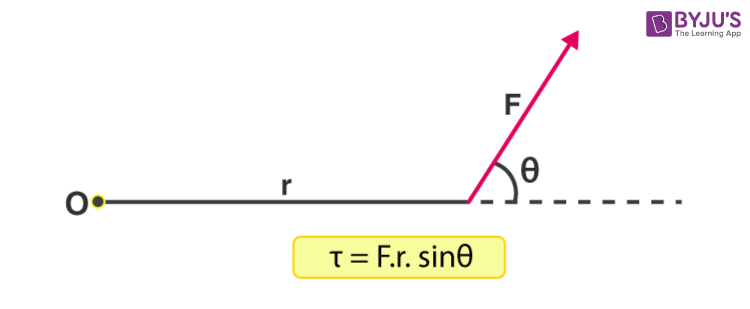
Measurement of Torque
The unit of torque is Newton–meter (N-m). The above equation can be represented as the vector product of force and position vector.
So, as it is a vector product hence torque also must be a vector. Using vector product notations we can find the direction of torque. We will consider an example to see how to calculate torque.
You may also want to check out these topics given below!
- Difference between Torque and Power
- Torque on an Electric Dipole
- Angular Momentum
- Torque on Current Loop
- Scalar Product and Vector Product
Examples of Torque
Let us consider the situation given below:
In the above diagram:
- F = 5 N
- r = 4 m
- sinθ = 30°
Putting these values we have,
τ = 5 x 4 x sin 30°
τ = 10 N·m
Some of the real-life examples involving torque are that of a see-saw or in automobiles engine. So next time when you go out just notice things that are working on the torque principle. We have just started our journey to learn rotational motion and translational motion. So sit back and enjoy learning with interesting video lessons.
What Is Torque in a Car?
Torque is the expression of a rotational or twisting force. The engines in vehicles rotate about an axis, thus creating torque. It can be viewed as the strength of a vehicle. Torque is what rockets a sports car from 0-60 kmph in seconds. Torque is also what powers big trucks hauling heavy loads into motion.
Applications of Torque
In any object experiencing torque, there is a pivot point. Some applications are provided below:
- Seesaws and Wrenches
- Gyroscopes
- A pendulum or a parachute is applying torque when swinging
- A person riding a bicycle
- Flag flying on a mast
See the video below to learn about the work done by torque
Frequently Asked Questions – FAQs
What is the difference between torque and moment?
Torque is a special case of moment, such that it relates to the axis of the rotation driving the rotation, whereas moment relates to being driven by an external force to cause the rotation.
Is torque energy?
No, torque is not energy.
How does torque differ from force?
Torque is a counterpart of force in rotational mechanics. The basic difference between them is that torque is the ability of a force to produce a twist around an axis.
What is the difference between torque in an electric medium and torque in a magnetic medium?
Torque is defined as the product of force and the perpendicular distance between the point of application of force and the pivot point. Torque in an electric medium means force experienced in an electric field. Similarly, torque in a magnetic medium is the force experienced in a magnetic field.
What are some examples of torque in everyday life?
If you wish to learn more physics concepts with the help of interactive video lessons, download BYJU’S – The Learning App.
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments