Schottky Defect

What is Schottky defect?

The Schottky defect (small shot effect) is named after a popular German physicist Walter H. Schottky who was even awarded the Royal Society’s Hughes medal in 1936 for the discovery of this defect.

In his model he explains that the defect is formed in ionic crystals when oppositely charged ions leave their lattice sites which leads to the creation of vacancies. These vacancies are further created to maintain a neutral charge in the crystal. The model further explains that the surrounding atoms also move to occupy these vacancies. Typically, when the defect is found in non-ionic crystals it is referred to as lattice vacancy defect.

Table of Contents

• Schottky Defect Definition
• Schottky Defect Explanation
• Characteristics of Schottky Defect
• Recommended Videos
• Schottky Defect Examples
• Schottky Defect Calculation
• Frequently Asked Questions – FAQs

Schottky Defect Definition

Schottky defect is a type of point defect or imperfection in solids which is caused by a vacant position that is generated in a crystal lattice due to the atoms or ions moving out from the interior to the surface of the crystal.

Schottky defect in crystals is observed when equal numbers of cations and anions are missing from the lattice. It is important that an equal number of cations and anions are missing, otherwise the electrical neutrality of the crystal will get affected.

Schottky Defect Explanation

Schottky defect is however different from frenkel defect wherein the atoms permanently leave the crystal in terms of schottky defect while atoms usually stay within the solid crystal in frenkel defect. We will further study the characteristics below.

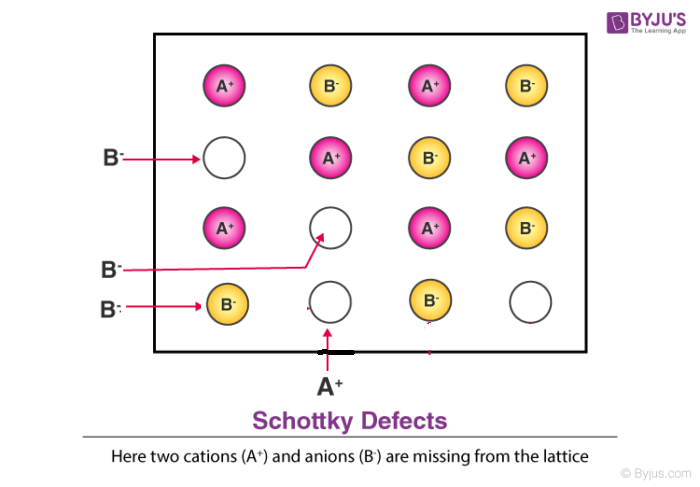
Characteristics of Schottky Defect

Some distinct characteristics of this defect are;

• There is a very small difference in size between cation and anion.
• Cation and anion both leave the solid crystal.
• Atoms also move out of the crystal permanently.
• Generally two vacancies are formed.
• As for the density of the solid it decreases considerably.

Recommended Videos

Schottky Defect Examples

It is a type of defect in crystals that mostly occurs in highly ionic compounds or highly coordinated compounds. The compound lattice has only a small difference in sizes between the anions and cations. Some common example of salts where Schottky defect is prominent include Sodium Chloride (NaCl), Potassium Chloride (KCl), Potassium Bromide (KBr), Caesium Chloride (CsCl) and Silver Bromide (AgBr).

Schottky Defect Calculation

The number of defects for an MX crystal can be calculated by the given formula;

where,

ns = number of Schottky defects per unit volume,

ΔH = enthalpy of defect formation,

R = gas constant,

T = absolute temperature (in K).

We can calculate N by using the formula;