Significant Figures Chemistry

What are Significant Figures?

In chemistry, Significant figures are the digits of value which carry meaning towards the resolution of the measurement. They are also called significant figures in chemistry.

All the experimental measurements have some kind of uncertainty associated with them. In order to ensure precision and accuracy in measurements and get real data, a fixed method to compensate for these uncertainties was required and this led to the significant figures. Before moving on to significant figures, let’s discuss the difference between precision and accuracy.

Significant Figures Chemistry

Significant Figures

Appropriate number of significant data is important in order to have a meaningful level of power-resolution when reporting analytical concentrations. Various methods or parameters can be used to determine how many significant figures are required. In most cases, three key figures are sufficient.

The term “significant figures” refers to the number of important single digits (0 to 9 inclusive) in the coefficient of expression in the scientific notation. The number of significant figures in the expression indicates the confidence or precision with which an engineer or scientist indicates a quantity.

Significant Figures Rules

There are certain rules which need to be followed to measure the significant figures of a calculated measurement.

Listed below are the basics of the law:

• All non-zero digits are significant.
• Zeroes between non-zero digits are significant.
• A trailing zero or final zero in the decimal portion only are significant.

Following are the significant figures rules that govern the determination of significant figures:

1. Those digits which are non-zero are significant.
   For example, in 6575 cm there are four significant figures and in 0.543 there are three significant figures.
2. If any zero precedes the non-zero digit then it is not significant. The preceding zero indicates the location of the decimal point, in 0.005 there is only one and the number 0.00232 has 3 figures.
3. If there is a zero between two non-zero digits then it is also a significant figure.
   For example; 4.5006 has five significant figures.
4. Zeroes at the end or on the right side of the number are also significant.
   For example; 0.500 has three significant figures.
5. Counting the number of objects for example 5 bananas and 10 oranges have infinite figures as these are inexact numbers.

Significant Figures Examples

The numbers in boldface are the significant figures.

• 4308 – 4 significant figures
• 40.05 – 4 significant figures
• 470,000 – 2 significant figures
• 4.00 – 3 significant figures
• 0.00500 – 3 significant figures

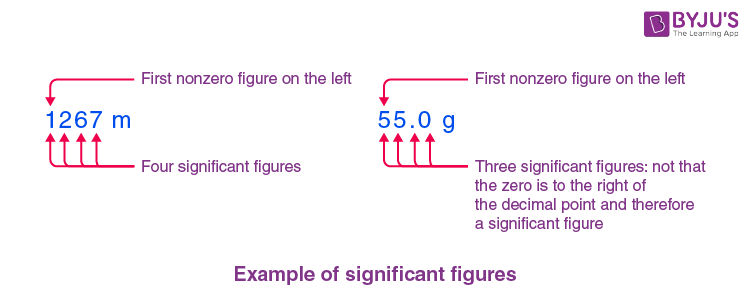
Example of Significant Figures

Let us learn a bit more about how the concept of significant figures comes into action with real-life applications.

1. Precision

The closeness of two or more quantities to each other is called precision. The level of measurement that gives the same result when repeated.

2. Accuracy

It is the level of measurement that gives true as well as consistent results (i.e. it has no systematic and random errors). The observed results are in agreement with the true results.

Examples

Let us understand this concept using an experiment, suppose the true mass for a ball is 5g and Ria takes two measurements in an experiment and reports the masses as 4.93 g and 4.95 g for the same ball. This reported values are precise but not accurate.

The number of significant figures is the meaningful digits which are known with certainty. The uncertainty is specified by writing uncertain as well as certain digits. If we take the example of a number 57.4, then 57 is certain and 0.4 is the uncertainty in measurement associated with the number

To learn more and read our other chemistry articles, download BYJU’S – The Learning App.