What is the work done by a variable force?
It is interesting to know that the forces we encounter every day are mostly variable in nature which is defined as a variable force. A force is said to perform work on a system if there is displacement in the system upon application of the force in the direction of the force. In the case of a variable force, integration is necessary to calculate the work done.
The work done by a constant force of magnitude F, as we know, that displaces an object by Δx can be given asL:
W = F.Δx
In the case of a variable force, work is calculated with the help of integration. For example, in the case of a spring, the force acting upon any object attached to a horizontal spring can be given as:
Fs = -kx
Where,
- k is the spring constant
- x is the displacement of the object attached
We can see that this force is proportional to the displacement of the object from the equilibrium position, hence the force acting at each instant during the compression and extension of the spring will be different. Thus, the infinitesimally small contributions of work done during each instant are to be counted in order to calculate the total work done.
The integral is evaluated as:
![]()
Force-Displacement Plot
The graphical interpretation of force in this force-displacement plot will help us understand this concept more clearly.
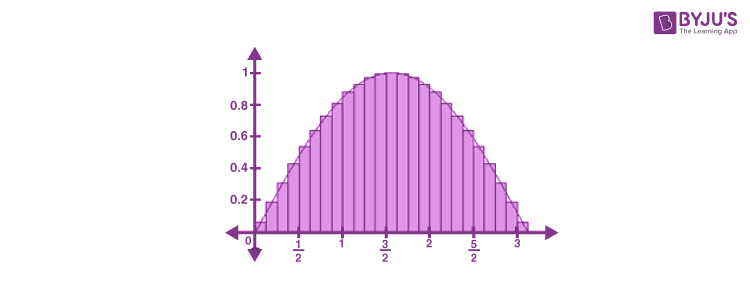
Consider the plot of variable force vs. displacement, as shown in the figure. Here the small divisions represent the displacement Δx due to the force F(x) acting at that point. Assuming the quantity Δx is small, then the force F(x) acting in that duration can be assumed as a constant force. The area enclosed by the rectangle of length equal to the magnitude of force F(x) and width equal to the displacement Δx, gives the work done by the force during that duration.
Mathematically, ΔW =F (x) Δx
Adding successive rectangles, the total work done can be written as,
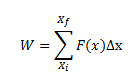
We assume the displacements to approach zero, the following equation gives the total work done by the force.
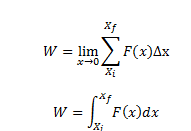
Thus, for a variable force, the work done can be expressed as a definite integral of force over displacement for any system.


thanks
Good