Young’s Double Slits Experiment Derivation

Introduction To Young’s Double Slits Experiment

During the year 1801, Thomas Young carried out an experiment where the wave and particle nature of light and matter were demonstrated. The schematic diagram of the experimental setup is shown below-

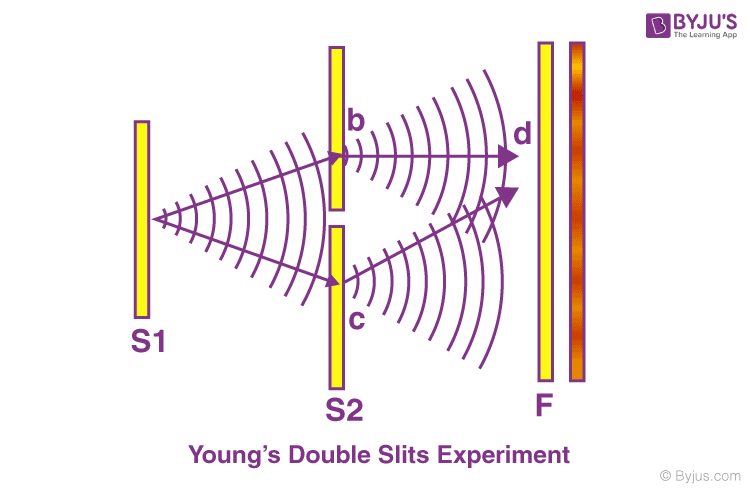
A beam of monochromatic light is made incident on the first screen, which contains the slit S₀. The emerging light then incident on the second screen which consists of two slits namely, S₁, S₂. These two slits serve as a source of coherent light. The emerging light waves from these slits interfere to produce an interference pattern on the screen. The interference pattern consists of consecutive bright and dark fringes. The dark fringes are the result of destructive interference and bright fringes are the result of constructive interference.

You may also want to check out these topics given below!

• Superposition of waves
• Diffraction
• Polarisation by scattering

• The light falls on the screen at the point P. which is at a distance y from the centre O.
• The distance between the double-slit system and the screen is L
• The two slits are separated by the distance d
• Distance travelled by the light ray from slit 1 to point P on the screen is r₁
• Distance travelled by the light ray from slit 2 to point P on the screen is r₂
• Thus, the light ray from slit 2 travels an extra distance of ẟ = r₂-r₁ than light ray from slit 1.
• This extra distance is termed as Path difference.

Refer to Figure(3) Applying laws of cosines; we can write –

∵ Cos(90° – θ) = Sinθ

Similarly,

∵ Cos(90° + θ) = -Sinθ

Subtracting equation (2) from (1) we get-

Let us impose the limit that the distance between the double slit system and the screen is much greater than the distance between the slits. That is L >> d. The sum of r₁ and r₂ can be approximated to r₁ + r₂ ≅2r. Thus, the path difference becomes –

In this limit, the two rays r₁ and r₂ are essentially treated as parallel. (See Figure(4))

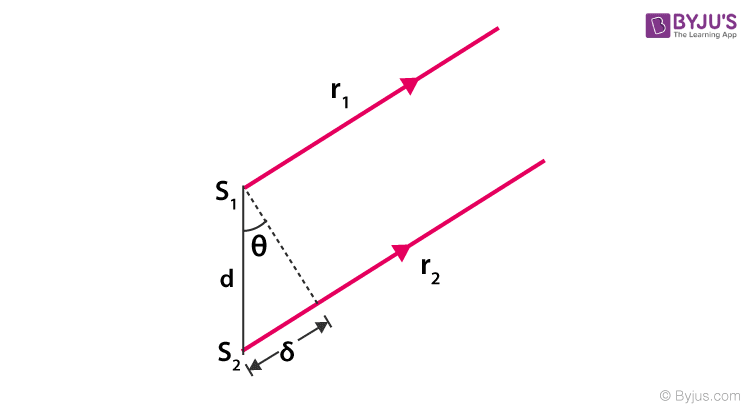
Figure(4): Assuming L >> d, The path difference between two rays.

To compare the phase of two waves, the value of path difference (ẟ) plays a crucial role.

Constructive interference is seen when path difference (𝛿) is zero or integral multiple of the wavelength (λ).

Where m is order number. The Zeroth order maximum (m=0)corresponds to the central bright fringe, here 𝜃=0. The first order maxima(m=±⁤1)(bright fringe) are on either side the central fringe.

Similarly, when 𝛿 is an odd integral multiple of λ/2, the resultant fringes will be 180⁰ out of phase, thus, forming a dark fringe.

Figure(5)(a) How path difference 𝛿 = λ/2 (m=0) results in destructive interference. (b) 𝛿 = λ (m=1) yields constructive inference.

Assuming the distance between the slits are much greater than the wavelength of the incident light, we get-

Substituting it in the constructive and destructive interference condition we can get the position of bright and dark fringes, respectively. The equation is as follows-

And