Orbitals - Orbital Energy & Orbital energy level

The energy of an electron in a single atom can be determined solely by the principal quantum number. Orbitals can be ranked in the increasing order of orbital energy as follows: 1s < 2s = 2p < 3s = 3p = 3d <4s = 4p = 4d= 4f. However, the energy of an electron in multi-electron atoms depends on both its principal quantum number (n) and its azimuthal quantum number (l). This difference in energy of various subshells residing in the same shell is mainly attributed to the mutual repulsion among the electrons in a multi-electron atom. In multi-electron atoms, there is a repulsive force acting between various electrons apart from the attractive force between the nucleus and the electrons. Thus, the stability of an electron in a multi-electron atom is dependent on the total attractive interactions and the repulsive interactions. The electron in an atom is only stable if the total attractive interaction is more than the total repulsive interaction. For bigger atoms, due to the presence of electrons in the inner shells, the electrons in the outer shell are deprived to experience the full positive charge of the nucleus (Z_e). This effect is known as the shielding of the outer shell electrons from the nucleus by the inner shell electrons. The net positive charge experienced by the outer shell electrons is termed as the effective nuclear charge (Zeff).

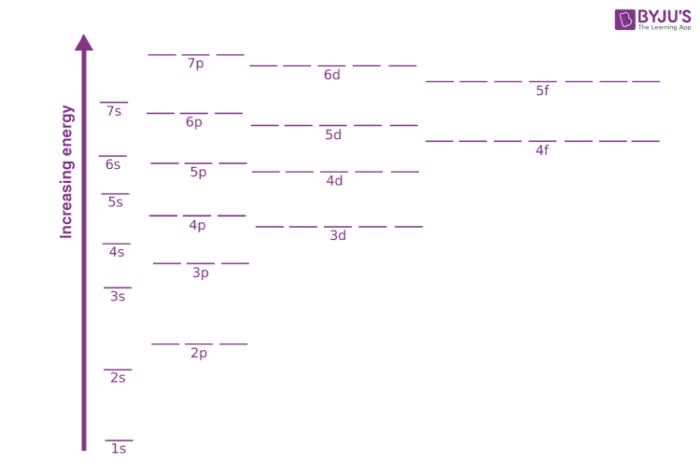
Fig: Energy variation for various orbitals

Factors affecting the energy of orbitals:

1. For a given value of the principal quantum number, the s orbital electron will be more tightly bound to the nucleus than the p orbital electron, which is more tightly bound in comparison to a d orbital electron.
2. S orbital electrons will have a lesser amount of energy (more negative) than that of p orbital electrons which will have lesser energy than that of d orbital electrons.
3. As the extent of shielding from the nucleus is different for electrons in different orbitals, it leads to the splitting of energy levels having the same principal quantum number. Thus, the energy of orbitals depends upon the values of both the principal quantum number (n) and the azimuthal quantum number (l). Hence, the lower the value of (n + l) for an orbital, the lower its energy. For the cases where we have two orbitals having the same value of (n + l), the orbital with a lower value of n (principal quantum number) will have the lower energy.
4. The energy of the orbitals in the same subshell decreases with an increase in the atomic number (Z_eff).

To learn more about the energies of orbitals download BYJU’S – The Learning App.