What is Band Theory of Metals?
Metals conduct electricity with the help of valence electrons present in them.
The atomic orbitals of the metals having the same energy combine to form molecular orbitals which are close in energy to each other to form a band.
In case, the band is partially filled or it overlaps with another higher energy unoccupied conduction band, electrons can easily flow under an applied electric field showing high conductivity.
Table of Contents
Band Theory of Metals Example
Let us take the example of sodium.
Sodium has an atomic configuration of 1s2, 2s2, 2p6, 3s1. It has one unpaired electron in the 3s orbital. The 3s valence atomic orbital of sodium overlaps with another such orbital of the same energy to form molecular orbitals. The atomic orbitals continue to combine in some fashion forming a band. The energy spread of this band is calculated as the difference in energy between the most strongly bound “bonding orbital” and the highest energy “anti bonding orbital”.
In other cases when the gap between the valence band and the conduction band (next higher unoccupied band) is quite high, electrons fail to jump from valence band to the conduction band. Such compounds show very less or no conductivity.
For example glass. When the gap between the valence band and conduction band is small, some electrons may jump from valence band to conduction band and thus show some conductivity. Such substances are known as semiconductors. For example silicon, germanium.
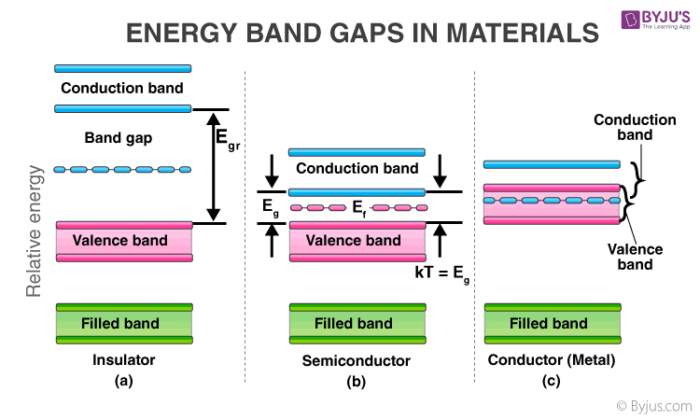
It is evident from the figure, in case of metal, there is no separation between the bands. This helps the incited electrons to easily move from one orbital to another and hence metals are good conductors of electricity. In the case of semiconductors, there is a small gap between the valence band and the conduction band.
Hence, only a small fraction of electrons (having sufficient energy) jumps when incited. However, we can increase the conductivity of such substances by increasing the temperature or doping. In insulators, the difference between the valence band and conduction band is very high. Hence, no conductivity is shown by such substances.
Recommended Videos

Frequently Asked Questions – FAQs
What is conduction band theory?
The conduction band is the band of electron orbitals that electrons can jump up into from the valence band when excited. When the electrons are in these orbitals, they have enough energy to move freely in the material. This movement of electrons creates an electric current.
How does band theory explain metallic character of lithium?
Electrons can be fed into one end of a metal wire and removed from the other end without causing any obvious change in the physical and chemical properties of the metal. … If two lithium atoms are brought together, the 1s core electrons remain essentially unchanged since there is virtually no overlap between them.
What is band theory of semiconductors?
According to the band theory, semiconductors will actually act as insulators at absolute zero. Above this temperature and yet still staying below the melting point of the solid, the metal would act as a semiconductor. Semiconductors are classified by the fully occupied valence band and unoccupied conduction band.
What is the band gap of conductor?
In a conductor there are no band gaps between the valence and conduction bands. In some metals the conduction and valence bands partially overlap. This means that electrons can move freely between the valence band and the conduction band.
What is free electron theory of metals?
The treatment of a metal as containing a gas of electrons completely free to move within it. The theory was originally proposed in 1900 to describe and correlate the electrical and thermal properties of metals.
For a detailed discussion on band theory, please visit BYJU’S.


Comments