Orbitals Chemistry

What are Atomic Orbitals?

Atomic orbitals are mathematical functions that describe the wave nature of electrons (or electron pairs) in an atom.

They offer a way to calculate the probability of finding an electron in a specified region around the nucleus of the atom.

Table of Contents

• Orbitals Chemistry
• Recommended Videos
• The Shape of s Orbitals
• The Shape of p Orbitals
• The Shape of d Orbitals
• Solved Example
• Frequently Asked Questions – FAQs

Orbitals Chemistry

There are four different kinds of orbitals, denoted s, p, d and f each with a different shape. Of the four, s and p orbitals are considered because these orbitals are the most common in organic and biological chemistry. An s-orbital is spherical with the nucleus at its centre, a p-orbitals is dumbbell-shaped and four of the five d orbitals are cloverleaf shaped. The fifth d orbital is shaped like an elongated dumbbell with a doughnut around its middle. The orbitals in an atom are organized into different layers or electron shells.

Recommended Videos

According to the quantum atomic model, an atom can have many possible numbers of orbitals. These orbitals can be categorized on the basis of their size, shape or orientation. A smaller sized orbital means there is a greater chance of getting an electron near the nucleus. The orbital wave function or ϕ is a mathematical function used for representing the coordinates of an electron. The square of the orbital wave function represents the probability of finding an electron.

This wave function also helps us in drawing boundary surface diagrams. Boundary surface diagrams of the constant probability density for different orbitals help us understand the shape of orbitals.

Let us represent the shapes of orbitals with the help of boundary surface diagrams:

The Shape of s Orbitals

• The boundary surface diagram for the s orbital looks like a sphere having the nucleus as its centre which in two dimensions can be seen as a circle.
• Hence, we can say that s-orbitals are spherically symmetric having the probability of finding the electron at a given distance equal in all the directions.
• The size of the s orbital is also found to increase with the increase in the value of the principal quantum number (n), thus, 4s > 3s> 2s > 1s.

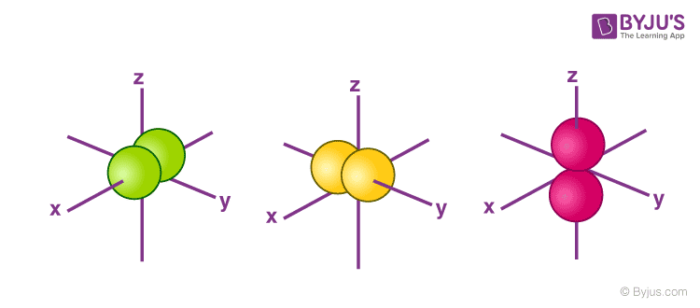
The Shape of p Orbitals

• Each p orbital consists of two sections better known as lobes which lie on either side of the plane passing through the nucleus.
• The three p orbitals differ in the way the lobes are oriented whereas they are identical in terms of size, shape, and energy.
• As the lobes lie along one of the x, y or z-axis, these three orbitals are given the designations 2p_x, 2p_y, and 2p_z. Thus, we can say that there are three p orbitals whose axes are mutually perpendicular.
• Similar to s orbitals the size, and energy of p orbitals increase with an increase in the principal quantum number (4p > 3p > 2p).

The Shape of d Orbitals

• The magnetic orbital quantum number for d orbitals is given as (-2,-1,0, 1,2). Hence, we can say that there are five d-orbitals.
• These orbitals are designated as d_xy, d_yz, d_xz, d_x²_–y ² and d_z².
• Out of these five d orbitals, the shapes of the first four d-orbitals are similar to each other, which is different from the d_z² orbital whereas the energy of all five d orbitals is the same.

Solved Example

Assuming 2s-2p mixing is NOT operative, the paramagnetic species among the following is :
(A) Be₂
(B) B₂
(C) C₂
(D) N₂

Solution:

The answer is C₂
C₂ = valence electrons =8
(σ2s)²(σ∗2s)²(σ2pz)²(π2px)¹(π2py)¹
Because if the question says 2s-2p orbital intermixing is not operative it indicates you to fill the molecular orbitals according to the energy order of the system having electrons >14
The electrons are unpaired in a bonding molecular orbital. Rest in all other molecules the electrons are paired all others are diamagnetic.