Shear Modulus Of Rigidity

What is Shear Modulus?

The shear Modulus of elasticity is one of the measures of the mechanical properties of solids. Other elastic moduli are Young’s modulus and bulk modulus. The shear modulus of material gives us the ratio of shear stress to shear strain in a body.

• Measured using the SI unit pascal or Pa.
• The dimensional formula of shear modulus is M¹L^-1T^-2.
• It is denoted by G.

It can be used to explain how a material resists transverse deformations but this is practical for small deformations only, following which they are able to return to the original state. This is because large shearing forces lead to permanent deformations (no longer elastic body).

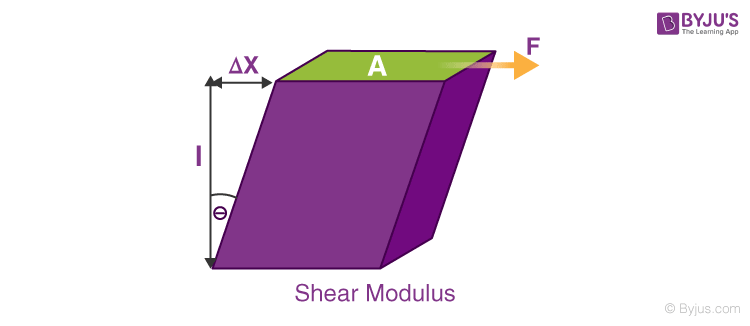
Modulus Of Rigidity Formula

\(\begin{array}{l}G=\frac{\tau _{xy}}{\gamma _{xy}}=\frac{\left ( \frac{F}{A} \right )}{\left ( \frac{\Delta x}{l} \right )}=\frac{Fl}{A\Delta x}\end{array} \)

Where,

• \(\begin{array}{l}\tau _{xy}=\frac{F}{A}\,is\,shear\,stress\end{array} \)
  .
• F is the force acting on the object.
• A is the area on which the force is acting.
• \(\begin{array}{l}\gamma _{xy}=\frac{\Delta x}{l}\,is\,the\,shear\,strain\end{array} \)
  .
• \(\begin{array}{l}\Delta x\,is\,the\,transverse\,displacement.\end{array} \)
• l is the initial length.

Units:

• The modulus of rigidity is measured using the SI unit pascal or Pa.
• Commonly it is expressed in terms of gigaPascal (GPa).
• Alternatively, it is also expressed in pounds per square inch(PSI).

Modulus Of Rigidity – Overview:

The modulus of rigidity is the elastic coefficient when a shear force is applied resulting in lateral deformation. It gives us a measure of how rigid a body is. The table given below briefs everything you need to know about rigidity modulus.

Definition	Shear modulus is the ratio of shear stress to shear strain in a body.
Symbol	G or S or μ
SI unit	Pascal (Pa), N/m2
Formula	Shear stress/shear strain
Dimension formula	M1L-1T-2

Example of Modulus Of Rigidity

The following example will give you a clear understanding of how the shear modulus helps in defining the rigidity of any material.

• Shear modulus of wood is 6.2×10⁸ Pa
• Shear modulus of steel is 7.2×10¹⁰ Pa

Thus, it implies that steel is a lot more (really a lot more) rigid than wood, around 127 times more!

Calculation:

A block of unknown material kept on a table(The square face is placed on the table.), is under a shearing force. The following data is given, calculate the shear modulus of the material.

Dimensions of the block = 60 mm x 60 mm x 20 mm

Shearing Force = 0.245 N
Displacement = 5 mm

Solution:

Substituting the values in the formula we get-

Shear stress

\(\begin{array}{l}=\frac{F}{A}=\frac{0.245}{60\times 60\times 10^{-6}}\end{array} \)

\(\begin{array}{l}=\frac{2450}{36}\, N/m^2\end{array} \)

Shear strain

\(\begin{array}{l}=\frac{\Delta x}{l}=\frac{5}{20}=\frac{1}{4}\end{array} \)

Thus, shear modulus,

\(\begin{array}{l}G=\frac{Shear\;stress}{Shear\;strain}\end{array} \)

\(\begin{array}{l}=\frac{2450\times 4}{36}=\frac{2450}{9}\end{array} \)

= 272.22 N/m².

You may also want to check out these topics given below!

• Relation Between Young’s Modulus And Bulk Modulus
• Elastomers
• Thermal stress
• Longitudinal Strain

Relation Between Elastic Constants

The elastic moduli of a material, like Young’s Modulus, Bulk Modulus, and Shear Modulus are specific forms of Hooke’s law, which states that, for an elastic material, the strain experienced by the corresponding stress applied is proportional to that stress. Thus, we can write the relation between elastic constants by the following equation:

2G(1+υ) = E = 3K(1−2υ)

Where,

• G is the Shear Modulus
• E is the Young’s Modulus
• K is the Bulk Modulus
• υ is Poisson’s Ratio

Frequently Asked Questions – FAQs

Q1

If the shear modulus of material 1 is x pascals and Material 2 is 30x pascals. What does it mean?

If the shear modulus of material 1 is x pascals and Material 2 is 30x pascals. It means that material 2 is more rigid than material 1.

Q2

What happens to the shear modulus if applied shear force increases?

The value of shear modulus is constant for a given material and is independent of the applied shear force.

Q3

How is rigidity modulus related to other elastic moduli?

The shear modulus is related to other elastic moduli as 2G(1+υ) = E = 3K(1−2υ)

where,

G is the Shear Modulus

E is the Young’s Modulus

K is the Bulk Modulus

υ is Poisson’s Ratio

Q4

What is meant by the modulus of rigidity?

The modulus of rigidity is defined as the ratio of shear stress to shear strain in a body.

Q5

What is the unit of shear strain?

Shear strain is a dimensionless physical quantity and hence has no unit.

Stay tuned with BYJU’S for more such interesting articles. If you wish to learn more physics concepts with the help of interactive video lessons, download BYJU’S – The Learning App.

The video explains the general stress-strain graph of an elastic material experiencing tensile load.

-->