Bohr model of the hydrogen atom was the first atomic model to successfully explain the radiation spectra of atomic hydrogen. Niels Bohr introduced the atomic Hydrogen model in the year 1913. Bohr’s Model of the hydrogen atom attempts to plug in certain gaps as suggested by Rutherford’s model. It holds a special place in history as it gave rise to quantum mechanics by introducing the quantum theory.
| Table of Contents |
Planetary Model of the Atom
Quantum mechanics emerged in the mid-1920s. Neil Bohr, one of the founders of quantum mechanics, was interested in the much-debated topic of the time – the structure of the atom. Numerous atomic models, including the theory postulated by J.J Thompson and the discovery of the nucleus by Ernest Rutherford, had emerged. But Bohr supported the planetary model, which asserted that electrons revolved around a positively charged nucleus just like the planets around the sun.
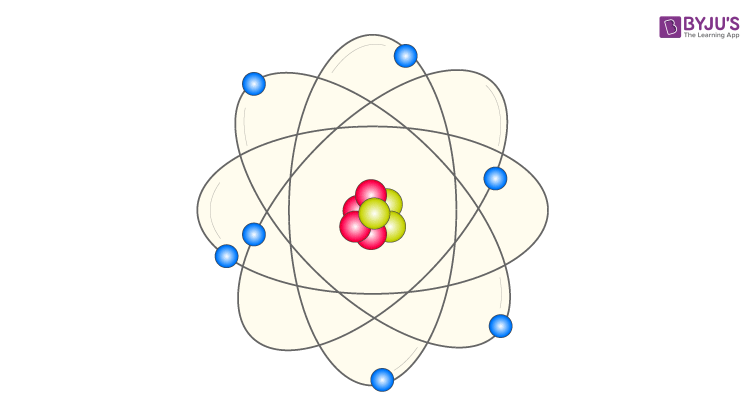
Planetary Model of The Atom
Nevertheless, scientists still had many unanswered questions such as
- Why didn’t the electrons drop into the nucleus as foretold by classical physics?
- Where are the electrons and what do they do there?
- How is the discrete emission lines produced by excited elements correlated to the internal structure of the atom?
Bohr addressed all these questions using a seemingly simple assumption: What if electron orbits and energies, could exhibit only specific values? You can check Atomic Theory to learn about the various atomic theory put forward by scientists in the early 20th century.
You may also want to check out these topics given below!
Bohr’s Equation
Bohr Model of the hydrogen atom first proposed the planetary model, but later an assumption concerning the electrons was made. The assumption was the quantization of the structure of atoms. Bohr’s proposed that electrons orbited the nucleus in specific orbits or shells with a fixed radius. Only those shells with a radius provided by the equation below were allowed, and it was impossible for electrons to exist between these shells.
Mathematically, the allowed value of the atomic radius is given by the equation:
\(\begin{array}{l}r(n)=n^2\times r(1)\end{array} \) |
Where,
- n is a positive integer
- r(1) is the smallest allowed radius for the hydrogen atom also known as the Bohr’s radius
The Bohr’s radius has a value of:
Bohr calculated the energy of an electron in the nth level of hydrogen by considering the electrons in circular, quantized orbits as:
\(\begin{array}{l}E(n)=-\frac{1}{n^2}\times 13.6\,eV\end{array} \) |
Where,
- 13.6 eV is the lowest possible energy of a hydrogen electron E(1).
The energy obtained is always a negative number and the ground state n = 1, has the most negative value. The reason being that the energy of an electron in orbit is relative to the energy of an electron that is entirely separated from its nucleus,
Absorption and Emission
According to Bohr’s model, an electron would absorb energy in the form of photons to get excited to a higher energy level. After escaping to the higher energy level, also known as the excited state, the excited electron is less stable, and therefore, would rapidly emit a photon to come back to a lower, more stable energy level. The energy of the emitted photon is equal to the difference in energy between the two energy levels for a specific transition. The energy can be calculated using the equation
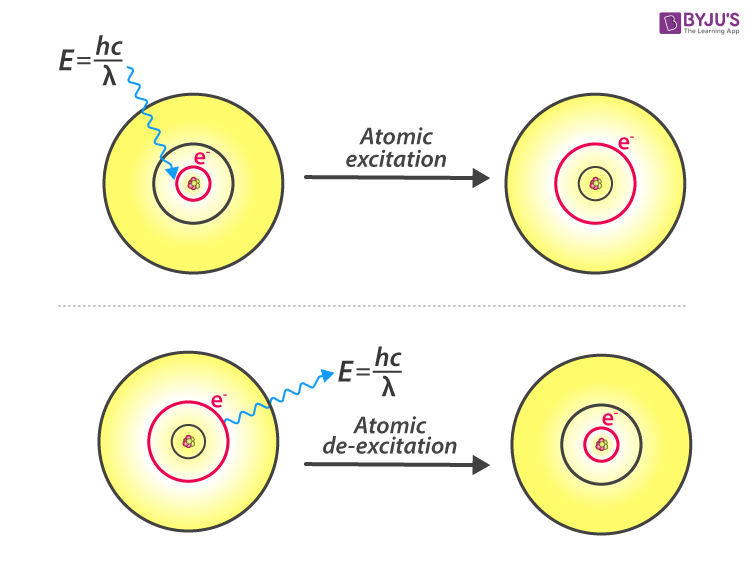
Atomic Excitation and De-excitation
Limitations of the Bohr Model of the Hydrogen Atom:
- Bohr’s model doesn’t work well for complex atoms.
- It couldn’t explain why some spectral lines are more intense than others.
- It could not explain why some spectral lines split into multiple lines in the presence of a magnetic field.
- Heisenberg’s uncertainty principle contradicts Bohr’s idea of electrons existing in specific orbits with a known radius and velocity.
Although the modern quantum mechanical model and the Bohr Model of the Hydrogen Atom may seem vastly different, the fundamental idea is the same in both. Classical physics isn’t sufficient to describe all the phenomena that occur on an atomic level. But, Bohr was the first to realise the quantization of electronic shells by fusing the idea of quantization into the electronic structure of the hydrogen atom and was successfully able to explain the emission spectra of hydrogen as well as other one-electron systems.
Summary:
- Bohr proposed that electrons travel in specific orbits, shells around the nucleus.
- According to Bohr’s calculation, the energy for an electron in the shell is given by the expression:
- The hydrogen spectrum is explained in terms of electrons absorbing and emitting photons to change energy levels, where the photon energy is:
- Bohr’s Model of the Hydrogen Atom isn’t applicable for systems with more than one electron.
If you wish to learn more Physics-concepts with the help of interactive video lessons, download BYJU’S – The Learning App.
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments