| Table of Contents |
A spectral series is a collection of sequentially grouped wavelengths. Which describes light or any electromagnetic radiation released by energised atoms
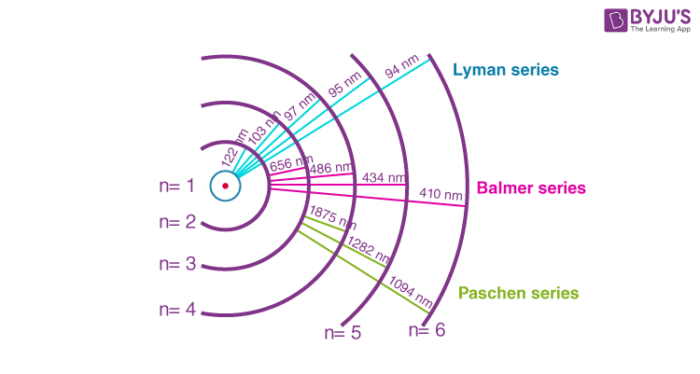
Figure(1): Spectrum of Hydrogen gas along with spectral series and respective wavelengths.
The hydrogen atom is the simplest atomic system found in nature; thus, it produces the simplest of these series. When the beam of light or any radiation is made to enter the device through a slit, each individual component of the light or radiation forms an image of the source. These images can be visualised when resolved under the spectroscope. The images will be in the form of parallel lines arranged next to each other with regular spacing. The lines will be farther apart on the higher wavelength side and gradually closer as they move from the higher to the lower wavelength side. The shortest wavelength with the fewest separated spectral lines is the series limit.
Rydberg Formula
Atomic hydrogen displays emission spectrum. This spectrum enfolds several spectral series. Once the electrons in the gas are excited, they transition between the energy levels. These spectral lines are the consequence of such electron transitions between energy levels modelled by Neils Bohr. The wavelengths of the spectral series are calculated by the Rydberg formula.
Rydberg formula relates to the energy difference between the various levels of Bohr’s model and the wavelengths of absorbed or emitted photons. It is mathematically expressed as-
Where,
- 𝜆 is the wavelength
- R is the Rydberg constant has the value 1.09737✕107 m-1
- Z is the atomic number
- nl is the lower energy level
- nh is the higher energy level
It should be noted that this equation applies to hydrogen and Hydrogen-like elements. Only when nh > nl does the equation return a significant value. The series categorisation by the Rydberg formula has played an important role in developing quantum mechanics. They’re also important in astronomical spectroscopy, particularly in detecting hydrogen and calculating redshift.
How Spectral Series Are Formed?
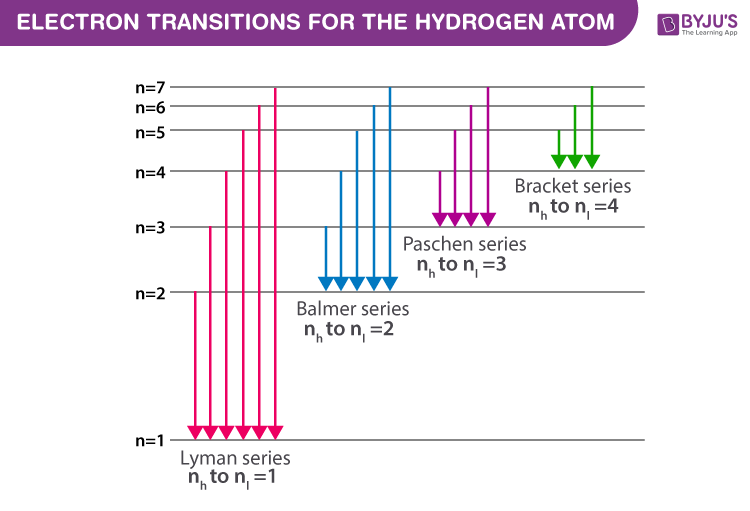
Figure(2): Electron transitions inside a Hydrogen atom
Every atom contains a set of energy levels/states that may be represented and explained using Bohr’s atomic model. He assigns quantum numbers to energy levels (n = 1,2,3,4,5,6…..). When electrons go from higher energy levels (nh) to lower energy ones (nl), they produce a photon with energy (nh – nl). Because the energy related to each state is set, the difference between the energy states is likewise fixed. Hence, the transition between identical energy levels produces the same energy photon.
The spectral series is broken into the corresponding series based on the electron transition to a lower energy state. The Greek alphabets are used within the series to segregate the spectral lines of corresponding energy. The spectral series of Hydrogen are:
Lyman Series (nl=1)
Theodore Lyman founded the series between 1906 and 1914. As a result, it is named for him. According to Bohr’s concept, the Lyman series appears when electrons shift from higher energy levels (nh = 2,3,4,5,6,…) to nl = 1 energy state. The wavelengths of the Lyman series are all in the ultraviolet range.
Refer to the table below for various wavelengths associated with spectral lines:
| Energy level (n) | Wavelength (𝜆 in nm) in vacuum |
| ∞ | 91.175 |
| 6 | 93.78 |
| 5 | 94.974 |
| 4 | 97.256 |
| 3 | 102.57 |
| 2 | 121.57 |
Balmer Series (nl=2)
The series was discovered in the year 1885 by Johann Balmer. Thus the series is named after him.
Balmer series is displayed when electron transition takes place from higher energy states(nh=3,4,5,6,7,…) to nl=2 energy state. All the wavelength of Balmer series falls in visible part of electromagnetic spectrum(400nm to 740nm). In astronomy, the presence of Hydrogen is detected using H-Alpha line of the Balmer series, and it is also a part of the solar spectrum.
Refer to the table below for various wavelengths associated with spectral lines.
| Energy level (n) | Wavelength (𝜆 in nm) in air |
| ∞ | 364.6 |
| 7 | 397.0 |
| 6 | 410.2 |
| 5 | 434.0 |
| 4 | 486.1 |
| 3 | 656.3 |
Paschen Series (nl=3)
The series was first observed in 1908 by German physicist Friedrich Paschen. Thus the series is named after him. Paschen series is displayed when electron transition takes place from higher energy states(nh=4,5,6,7,8,…) to nl=3 energy state. All the wavelength of the Paschen series falls in the Infrared region of the electromagnetic spectrum. The shortest wavelength of the next series, i.e., the Brackett series, overlaps with the Paschen series. From this series, all subsequent series overlap.
Refer to the table below for various wavelengths associated with spectral lines.
| Energy level (n) | Wavelength (𝜆 in nm) in air |
| ∞ | 820.4 |
| 8 | 954.6 |
| 7 | 1005 |
| 6 | 1094 |
| 5 | 1282 |
| 4 | 1875 |
Brackett Series (nl=4)
The series was first observed in 1922 by American physicist Friedrich Sumner Brackett. Thus the series is named after him. Brackett series is displayed when electron transition takes place from higher energy states(nh=5,6,7,8,9…) to nl=4 energy state. All the wavelength of the Brackett series falls in the Infrared region of the electromagnetic spectrum.
Refer to the table below for various wavelengths associated with spectral lines.
| Energy level (n) | Wavelength (𝜆 in nm) in air |
| ∞ | 1458 |
| 9 | 1817 |
| 8 | 1944 |
| 7 | 2166 |
| 6 | 2625 |
| 5 | 4051 |
Pfund Series (nl=5)
The series was first observed during the year 1924 by August Harman Pfund. Thus, the series is named after him. Pfund series is displayed when electron transition takes place from higher energy states(nh=6,7,8,9,10,…) to nl=5 energy state. All the wavelength of Pfund series falls in Infrared region of the electromagnetic spectrum.
Refer to the table below for various wavelengths associated with spectral lines.
| Energy level (n) | Wavelength (𝜆 in nm) in vacuum |
| ∞ | 2279 |
| 10 | 3039 |
| 9 | 3297 |
| 8 | 3741 |
| 7 | 4654 |
| 6 | 7460 |
Humphreys Series (nl=6)
The series was first observed in 1953 by American Physicist Curtis J Humphreys. Thus, the series is named after him. Humphreys series is displayed when electron transition takes place from higher energy statesnh=7,8,9,10,11…) to nl=6 energy state. All the wavelength of the Humphreys series falls in the Infrared region of the electromagnetic spectrum.
Refer to the table below for various wavelengths associated with spectral lines.
| Energy level (n) | Wavelength (𝜆 in μm) in vacuum |
| ∞ | 3.282 |
| 11 | 4.673 |
| 10 | 5.129 |
| 9 | 5.908 |
| 8 | 7.503 |
| 7 | 12.37 |
They are the unnamed series which follow the spectral pattern described by the Rydberg equation. They were first observed in the infrared range during an experiment in 1972 by Peter Hanson and John Strong. These series are displayed when electron transition takes place from higher energy states(nh=8,9,10,11…) to nl=7 or above energy state. The series is observed in a higher wavelength. The spectral lines are extremely faint and widely spread out. They correspond to highly rare atomic events.
Related Physics Links:
| Spectroscopy |
| X-Ray |
| Wavelength of light |
Watch the video and understand the relationship between frequency and wavelength

Frequently Asked Questions – FAQs
What is the significance of the Rydberg formula?
What is a spectral series?
What is a photon?
Which is the simplest atomic system found in the Universe?
Who discovered the Lyman series?
Which are the main spectral series?
Stay tuned with BYJU’S for the latest Physics-related topics.


Comments